Seja a função, definida em
Dada por
Determine equações para as curvas de nível de quando . Faça um esboço delas (em linha cheia) e da restrição no domínio (em pontilhado).
Passo 1
Vamos começar entendendo o domínio dessa função, afinal, se a função não estiver definida num ponto, nenhuma curva de nível poderá passar por ele.
A região do domínio é
Rearrumando isso, temos
Que nada mais é do que uma parábola. Assim, o domínio de é todo o plano, exceto os pontos que estiverem sobre a parábola
Passo 2
Ótimo! Agora vamos determinar as curvas de nível.
Para isso, basta igualarmos a expressão da função aos valores de pedidos.
Para , a curva de nível é:
Completado quadrados, temos:
Dividindo tudo por 4:
Temos então que a curva de nível zero da função é a elipse acima.
Passo 3
Agora, para , a curva de nível é:
Que é uma parábola, só que em torno de .
Passo 4
Por fim, para , a curva de nível é:
Que é uma hipérbole.
Como o eixo é o que está com sinal positivo, então, ele corta a hipérbole em seus vértices.
Passo 5
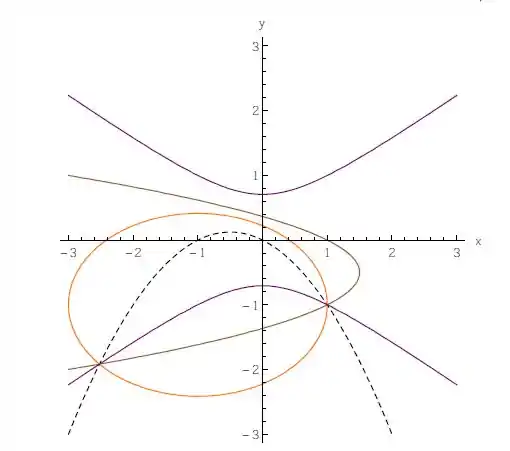
Agora só nos resta esboçar tudo isso junto.
Assim, esboçando a elipse
Com centro em e semi eixos e ,
Esboçando a parábola
Cortando o eixo .
Esboçando a hipérbole
Cortando o eixo .
E, esboçando a parábola que delimita o domínio
Temos
Resposta
Domínio:
Curvas de nível: