USP, São Carlos, Calculo 2, Listas de C2 - Grupo Coordenado 2022 - Lista 3 - Módulo 3, Questão 10a
10. Descreva a superfície de nível para :
(a)
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema queremos as curvas de nível da função nos níveis .
Lembra como fazemos isso? 🤔
O que temos que fazer é igualar a função a uma variavel que representa o nível da função que temos que representar...
Assim temos que atribuir a os valores e em cada equação formada, vamos ter um gráfico tridimensional que vamos ter que representar no espaço cartesiano.
Sacou? Bora ver como é na prática! 😉
Passo 2
Igualando a função a , temos
Isolando em um dos lados, vamos obter
Dessa forma, como não varia em , vamos obter uma curva bidimensional e para representar no espaço, podemos projetar essa curva ao longo de ...
Por exemplo, para
Para não podemos usar a mesma equação, ou seja
E para
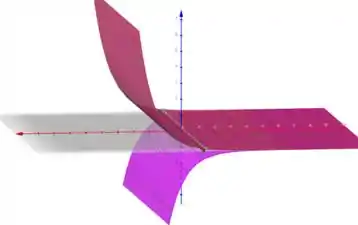
Esboçando essas equações no espaço, vamos obter
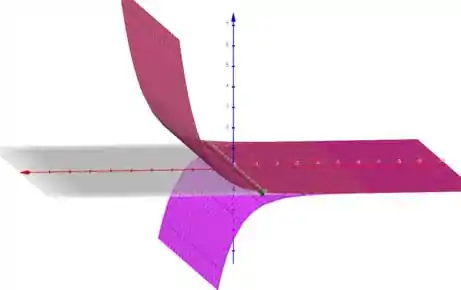
O que achou? Foi de boa? Responde aí! 😊
Resposta
