USP, São Carlos, Calculo 2, Listas de C2 - Grupo Coordenado 2022 - Lista 3 - Módulo 3, Questão 8e
8. Esboce os gráficos das funções abaixo. Reconheça todos os gráficos, exceto um, como superfícies dadas por (ou contidas em) quadráticas, identificando-as:
(e)
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema queremos apenas esboçar o gráfico da função .
Lembra como fazemos isso? 🤔
Podemos esboçar o gráfico de esboçando algumas curvas de níveis da função.
Fazendo , podemos fixar uma das variáveis como um valor, assim vamos obter uma equação que representa um gráfico bidimensional...
Esboçando vários gráficos bidimensionais cada um contido no plano da variavel cujo valor foi fixado, podemos obter uma ideia de como a função se comporta no espaço.
Sacou? Bora ver como é na prática! 😉
Passo 2
Fazendo , temos
Perceba que elevando os dois lados ao quadrado, vamos obter
Veja que a equação obtida é exatamente igual a equação da circunferência centrada na origem onde no nosso caso, .
Dessa forma, atribuindo valores para , podemos ver como a função se comporta no espaço.
Por exemplo fazendo
Agora
E por fim,
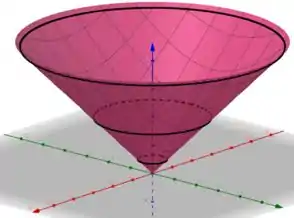
Juntando essas curvas no espaço cada uma em seu devido plano, temos
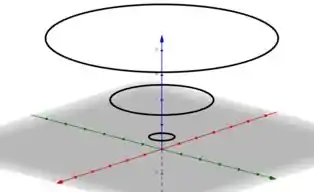
Esboçando o gráfico de a partir dessas curvas, temos
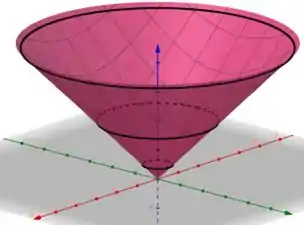
Sacou como faz? Responde Aí! 😉
Resposta
