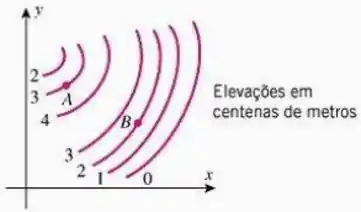
Em cada parte, as questões se referem ao mapa de contorno na figura abaixo.

a) O ponto ou é o ponto mais alto? Explique seu raciocínio.

b) O ponto ou está na inclinação mais íngreme? Explique seu raciocínio.

c) Iniciando em e movendo-se de tal modo que permanece constante e cresce, a elevação começará a crescer ou decrescer?

d) Iniciando em e movendo-se de tal modo que permanece constante e cresce, a elevação começará a crescer ou decrescer?

e) Iniciando em e movendo-se de tal modo que permanece constante e decresce, a elevação começará a crescer ou decrescer?

f) Iniciando em e movendo-se de tal modo que permanece constante e decresce, a elevação começará a crescer ou decrescer?

b)

Quanto mais próximas as curvas de nível, mais íngreme a inclinação.

Podemos ver que as curvas de nível em torno de estão mais próximas, logo o ponto está na inclinação mais íngreme.

c)

Como já vimos, o ponto está na altura .

Se partirmos dele mantendo o constante e fazendo o crescer, ou seja, pra direita, estaremos caminhando na direção de uma curva de nível de altura .

Portanto, a elevação está crescendo!

d)

Seguindo a mesma lógica da letra anterior, partindo do ponto pra direita estamos andando da altura na direção de uma curva de altura : a elevação está decrescendo.

e)

É a mesma coisa! Partindo de mantendo o constante e fazendo o decrescer, estamos andando pra baixo, na direção da mesma curva de nível de altura do item c): a elevação está crescendo.

f)

E agora, pra finalizar, indo do ponto pra baixo notamos que a elevação está decrescendo: de novo estamos andando de uma curva de nível pra uma de nível .