UERJ, Sem Campus, Cálculo II, Listas de C2 - Profº Ditter Adolfo - 1ª Lista, Questão 2f
2) Representar no plano cartesiano as curvas de nível das funções abaixo correspondentes aos valores de nível dados
(f) , , e .
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema, temos que calcular e esboçar no plano cartesiano as curvas de níveis solicitadas da função .
Tem ideia de como fazemos isso? 😬
Para esboçar a curva de nível de uma função, temos que igualar a , onde representa a curva de nível que vamos substituir.
Na prática, temos uma função tridimensional e é o plano paralelo ao plano de altura em . Esse plano corta a função em algum momento e esse corte gera uma curva bidimensional, sendo essa curva nossa curva de nível!
Sacou? Bora começar! 😎
Passo 2
A função foi dada como
E os níveis que vamos obter são , e .
Igualando , temos
Perceba que essa equação é muito parecida com a equação da circunferência centrada na origem,
Dessa forma, podemos imaginar que nossas curvas de níveis serão circunferências com raio .
Tranquilo até aqui? 😎
Passo 3
Agora vamos obter as curvas solicitadas no enunciado...
Para
Para
E para
Esboçando essas curvas no plano cartesiano, vamos obter
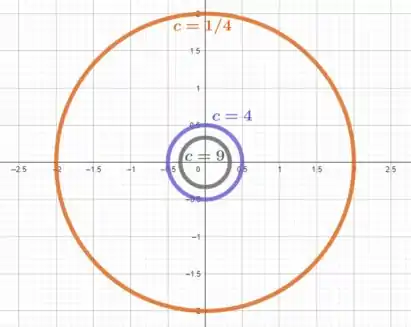
O que achou? Foi de boa? Responde aí! 😊
Resposta
