Desenhe as curvas de nível e determine a imagem:
Passo 1
Antes de determinar as curvas de nível, é importante saber qual o domínio da função!
Repara que temos uma fração, então o denominador não pode zerar, ou seja,
Deste modo, temos que a função não é definida no ponto , pois zeraríamos o denominador.
Vamos por partes! Pra achar as equações dessas curvas de nível temos que igualar a função a uma constante qualquer :
Vamos lá!
Passo 2
Vamos tentar isolar o , deixando ele em função de :
Beleza, aí está nossa equação explícita! Agora vamos analisar possíveis valores de
Passo 3
Começando pelo caso mais simples: . Isso dá simplesmente
que é uma reta bem fácil de esboçar:
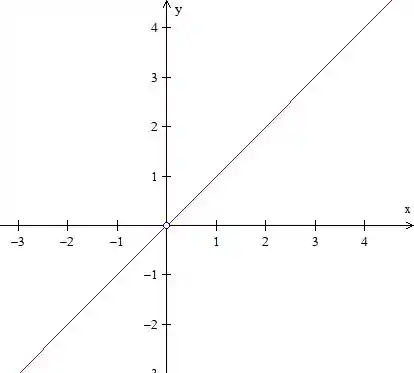
Repare que nossa função não está definida no ponto , por isso tem essa bolinha aberta ai na origem, já que se a função não tá definida num ponto, a curva de nível não pode passar por esse ponto, beleza?
Passo 4
Outro caso bem tranquilo é a curva de nível :
que nada mais é que o eixo :
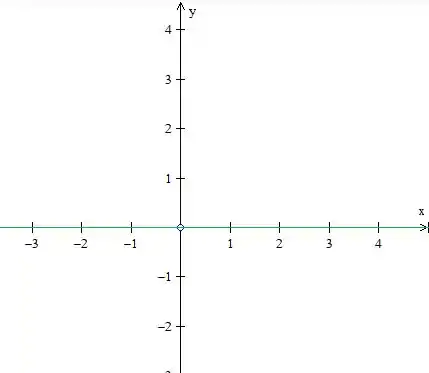
Passo 5
Vamos fazer mais umas curvas de nível que tá de bom tamanho. Vamos pegar um
Podemos usar agora :
Também sem grande mistério pra desenhar:
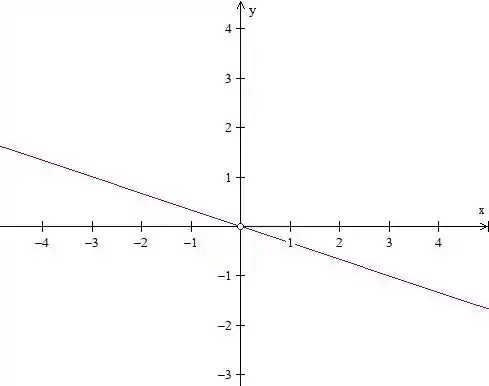
Passo 6
E agora, pra finalizar, que tal uma curva de nível com negativo?
Usemos então . Como não podemos zerar o denominador, vamos olhar a função de outra forma,
Fazendo :
Tranquilho?!
O desenho é:
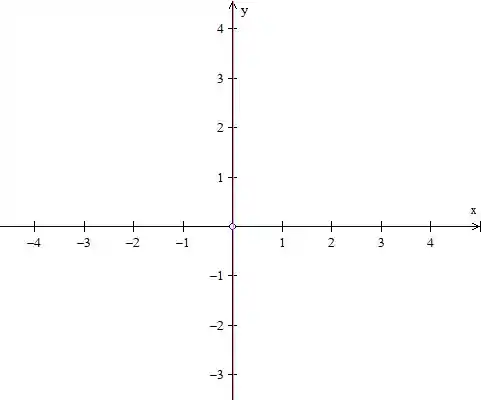
Passo 7
Juntando todas as curvas de nível que desenhamos:
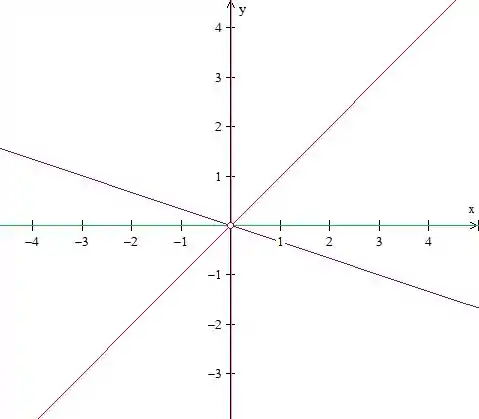
Passo 8
Maas ainda não acabou a questão! Ele pediu também a imagem da função, lembra?
Relembrando, a imagem é o conjunto de todos os valores que a função pode assumir. E o fato da gente já ter olhado as curvas de nível da função vai ajudar bastante!
A função pode valer para vários valores de :
E o conjunto desses que vai ser a imagem da função.
Então temos que descobrir quais valores de são permitidos e quais não são. E na verdade já fizemos isso! Porque esse é a mesma coisa que a gente fez pra achar as curvas de nível, e acabou resultando na equação
Aí vimos que pode valer qualquer coisa, inclusive .
Ou seja, a função pode assumir qualquer valor real, então sua imagem é o conjunto dos reais.
Resposta
Curvas de nível:
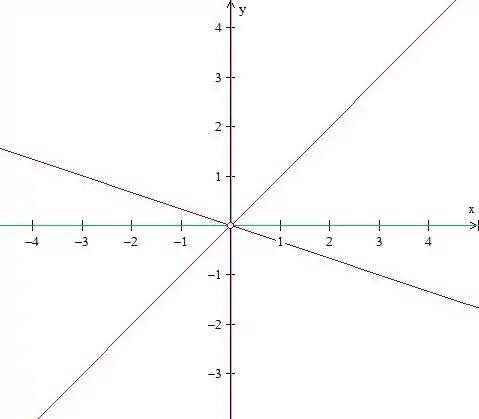
Imagem: