USP, São Carlos, Calculo 2, Listas de C2 - Grupo Coordenado 2022 - Lista 3 - Módulo 3, Questão 9f
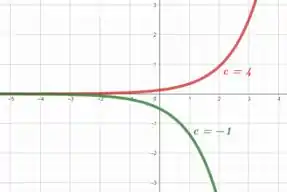
9. Em cada item, esboce no mesmo plano coordenado as curvas de nível para :
(f)
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema queremos as curvas de nível da função nos níveis .
Lembra como fazemos isso? 🤔
O que temos que fazer é igualar a função a uma variavel que representa o nível da função que temos que representar...
Assim temos que atribuir a os valores e em cada equação formada, vamos ter um gráfico bidimensional que vamos ter que representar no plano cartesiano.
Sacou? Bora ver como é na prática! 😉
Passo 2
Igualando a função a , temos
Isolando em um lado da igualdade, vamos obter que
Podemos perceber que para cada valor de vamos ter uma exponencial de índice ...
Por exemplo, para
Para não podemos usar a mesma equação, ou seja
E para
Esboçando essas equações no plano cartesiano, vamos obter
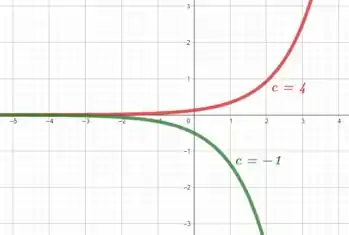
Sacou como faz? Responde Aí! 😉
Resposta
