UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille - Segunda Lista de Exercícios, Questão 22f
Descreva e esboce as curvas de nível e o gráfico da função:
Passo 1
Faaaala gente bonita, tudo bem com vocês?
Nessa questão recebemos a função de duas variáveis dada por:
E, precisamos determinar a curva de nível dessa função, bem como o seu gráfico.
Pra determinar a curva de nível basta igualarmos a função dada a uma constante. A partir disso, analisamos a curva que será formada no plano.
Já para determinar o gráfico da função de duas variáveis, precisamos analisar a figura tridimensional que a nossa lei de função irá gerar.
Vem com a gente que esses passos vão ficar super claros 😊
Passo 2
Começando pela curva de nível, precisamos trocar por uma constante na sua lei de formação.
Assim:
Ou seja:
Fazendo:
A equação pode ser reescrita, como:
Essa é a equação de uma elipse, centrada em , e com semi-eixos valendo e .
Essa elipse é justamente a curva de nível de .
Podemos esboçá-la como:
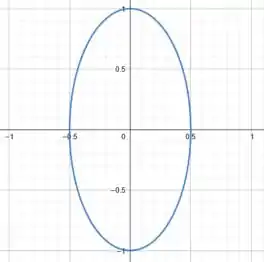
(consideramos para desenhar o gráfico).
Passo 3
Vamos agora determinar o gráfico da função. Temos:
Como já sabemos que a curva de nível é uma elipse, podemos imaginar que o gráfico da função é formado pela superposição dessas curvas de nível, onde cada uma delas tem o valor da constante um pouco maior.
Assim, esperamos ter uma espécie de cone onde em , ele se restringe a um ponto.
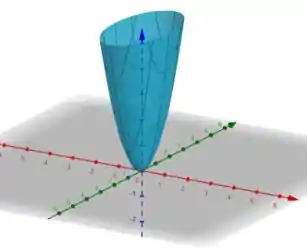
Prontinho gente! É isso aí!
Até a próxima ���
Resposta
Resposta no texto.