13. Se dá a temperatura num ponto sobre uma placa delgada de metal no plano-, , então as curvas de nível de são chamadas de curvas isotérmicas (todos os pontos sobre cada uma dessas curvas possuem a mesma temperatura). Suponha que uma placa ocupe o primeiro quadrante e .
(b) Uma formiga, inicialmente no ponto , se move sobre a placa de modo que a temperatura ao longo de sua trajetória permanece constante. Qual é essa trajetória, e qual é a temperatura correspondente?
Passo 1
Iae! Como vai, meu querido? 😁 Bora aprender mais uma questão? 😉

Nesse problema foi dada uma função temperatura sobre uma superfície e nessa superfície temos uma formiga em e essa formiga se move sobre a placa de modo que a temperatura sobre ela permanece a mesma.
A partir daí queremos obter a temperatura sobre a formiga e qual é a trajetória que ela pode percorrer.
Parece complicado? 🤔
Dada a função podemos obter o valor de aplicando o ponto em .
Já para obter a trajetória que a formiga pode percorrer, temos que fazer e substituir pelo valor que calculamos anteriormente e assim vamos obter uma equação bidimensional.
Esboçando essa equação no plano cartesiano, vamos obter a trajetória.
Sacou? Bora começar! 😉
Passo 2
Se , então
Logo, a temperatura sobre a formiga é unidades.
Agora fazendo , vamos obter
Isolando em um lado da igualdade...
Perceba que essa equação descreve uma hipérbole, ou seja.
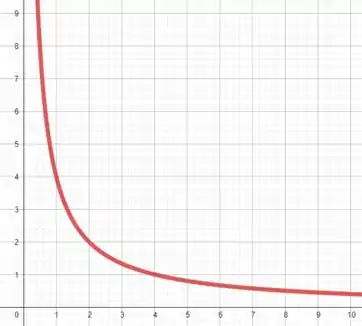
Pegou o esquema? Responde Aí! 😁
Resposta