2) considere a função .
a) Esboce, no plano cartesiano abaixo, o domínio de , indicando pontos que não pertençam ao seu domínio com linhas tracejadas. Determine as curvas de nível e de e esboce suas imagens, também no plano abaixo.
b) Decida, justificando, se existe.
Passo 1
a) A função não está definida para valores de , assim para a curva de nível , temos:
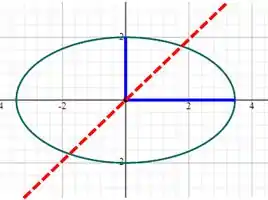
E para
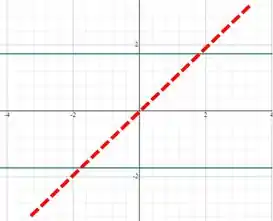
Passo 2
b) Para determinar se o limite existe a primeira coisa que faremos é substituir os valores de tendência de e diretamente na função e verificar se conseguimos calcular esse limite.
Assim, como
Como e se aproximam juntos de , o denominador não tenderá a zero, ele será igual a zero e isso torna nosso limite impossível de ser calculado dessa forma.
Então, suspeitamos que esse limite não existe.
Passo 3
Vamos tentar calcular esse limite de outra forma, fazendo uma substituição de e calcular o limite através desse caminho:
Que arrumando um pouco melhor, se torna:
Simplificando, ficamos com:
E calculando o limite, teremos:
Maravilha, agora vamos tentar ver outro caminho, fazendo uma substituição de e calcular o limite através desse caminho:
Que arrumando um pouco melhor, se torna:
Simplificando, ficamos com:
E calculando o limite, teremos:
Perceba que os limites calculados por dois caminhos diferentes deram resultados diferentes, então concluímos que o limite não existe.
Prontinho!!
Resposta
Resposta:
a) No desenvolvimento
b) O limite não existe.