Seja
a) Determine e esboce a curva de nível de que passe pelo ponto (1,1).
b) Determine e esboce a curva de nível de que passe pelo ponto (1,1).
c) A afirmação “As curvas de nível de e dos itens anteriores são ortogonais no ponto (1,1)” é verdadeira ou falsa? Justifique sua resposta.
Passo 1
a) Para descobrirmos como é a curva de nível, precisamos antes saer qual nosso k, ou seja, o valor de z naquela curva. Como a questão quer a curva que passe pelo ponto (1,1), teremos:
Isolando o y temos:
Desenhando então a função
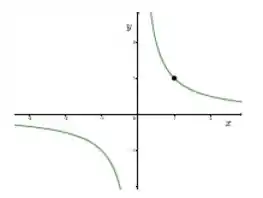
Tranquilinho, né? Bora pra letra b.
Passo 2
b) Fazendo a mesma coisa, mas agora com a
Isso aí nos dá uma circunferência de raio.
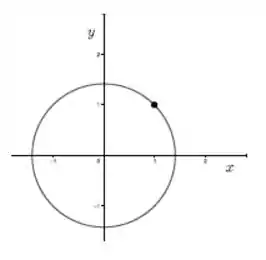
Passo 3
c) “As curvas de nível de e dos itens anteriores são ortogonais no ponto (1,1)”
Para verificar isso, precisamos que o produto escalar dos vetores normais de e no ponto seja nulo!
Calculando então primeiramente o vetor normal de no ponto , que é fazendo o gradiente de :
E aplicando o ponto:
Fazendo o mesmo para
Aplicando ao ponto
Se calcularmos o produto escalar entre e :
Isso é diferente de zero, logo, as curvas não são ortogonais.
Resposta
Ei, a resposta está no passo a passo :)