UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille - Segunda Lista de Exercícios, Questão 22c
22. Descreva e esboce as curvas de nível e o gráfico da função:
c)
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema queremos obter algumas curvas de níveis da função e esboçar o gráfico dessa função.
Tem ideia de como fazemos isso? 🤔
As curvas de nível de uma função são conjuntos de pontos no plano onde a função tem um mesmo valor de . Ou seja, as curvas de nível são os conjuntos de pontos que satisfazem a equação , onde é um valor do eixo .
Para plotar as curvas de nível de uma função, podemos utilizar um gráfico bidimensional no plano e traçar as curvas que correspondem a cada valor de da função.
Sacou? Bora começar! 😁
Passo 2
Vamos começar definindo alguns valores de para substituir na função
Podemos usar , e .
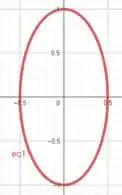
Para , temos
Perceba que essa equação é exatamente a equação da elipse com e
Só recapitulando, a equação genérica de uma elipse é dada por
Onde e são os raios em e em da elipse e e são as coordenadas do centro da elipse.
Portanto, essa equação resulta em uma elipse de , e centro em .
Plotando essa curva temos...
Entendeu essa parte? 😊
Passo 3
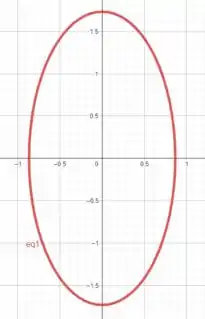
Agora vamos fazer a mesma coisa para
Nessa equação temos também uma circunferência centrada em , com e .
Plotando essa curva, vamos obter
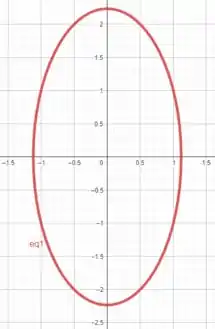
E por último, fazendo
Plotando essa curva em com e com centro em .
Bacana, não é? 😁
Passo 4
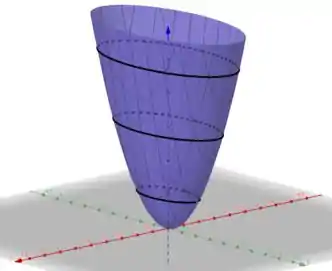
E finalmente, podemos usar essas curvas de níveis para determinar o gráfico de em três dimensões.
Esboçando cada curva em seu respectivo nível de e estimando o comportamento da função entre um nível e outro, vamos chegar em
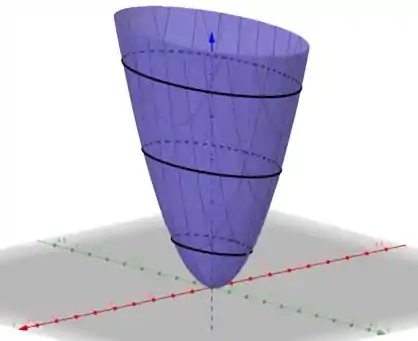
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
