UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Marcos André - 1ª Lista de Exercícios, Questão 1d
Determine o domínio da função dada e represente-o graficamente. Esboce duas curvas de nível para cada função.
Passo 1
Faaaaala pessoal, tudo numa boa com vocês?
Nessa questão recebemos a função de duas variáveis dada por:
Sobre essa função precisamos determinar o seu domínio e representar o conjunto desse domínio graficamente. Além disso, também precisamos esboçar duas curvas de nível dessa função.
Beleza?!
Tá, mas vamos com calma em cada uma dessas coisas. Primeiramente, vocês lembram o que é o domínio?
Então, nada mais é do que o conjunto de pontos que podem servir de entrada na nossa função sem que a gente tenha algum absurdo matemático. Ou seja, na prática precisamos verificar os pontos que são restrição na nossa função.
Já as curvas de nível podemos calcular igualando a função a uma constante, tipo assim:
Daí, o enunciado nos pede para colocar dois valores pra essa constante e esboçar a curva formada.
Show de bola! Vamos começar analisando se tem alguma restrição no domínio da nossa função e depois esboçamos o conjunto e as curvas de nível!
Vem comigo 😊
Passo 2
Bom, temos a função:
Pra analisar o seu domínio devemos ter em mente que funções envolvendo raiz quadrada têm uma restrição: o radicando precisa sempre ser maior ou igual a zero. Assim:
Assim, temos duas soluções:
Ou seja, o e o quadrante do nosso plano cartesiano. Logo, temos o seguinte conjunto para o domínio:
E, o seguinte esboço:
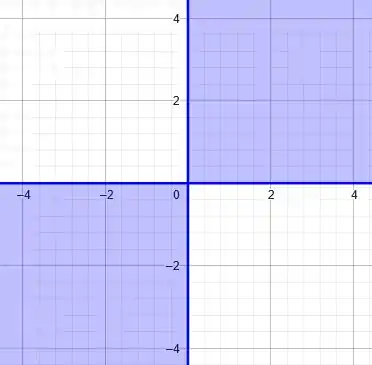
Perfeito!
Passo 3
Vamos agora para as curvas de nível. Como vimos no passo , elas obedecem à seguinte equação:
Escolhendo , podemos esboçar a primeira curva de nível:
É a equação de uma hipérbole.
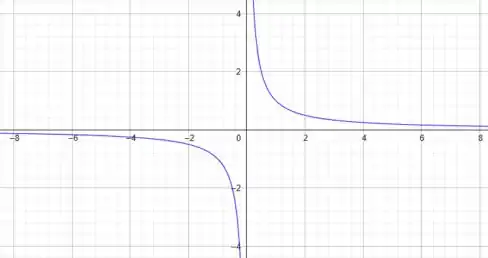
Já se escolhermos , vamos ter:
Que também é uma hipérbole.
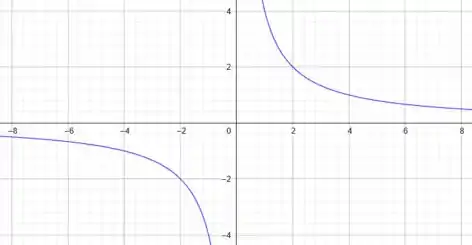
Perfeito galera! Entenderam direitinho?
Até a próxima gente 😊
Resposta
Resposta no texto.