Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Curvas de Nível

Ver Teoria
Exercício 912345678101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Funções de Várias Variáveis

Considere F x , y = 10 x 2 - 2 y x 2 + y 2 . Determine o domínio de F e esboce as curvas de níveis c = 0 , c = 1 e c = 10

Passo 1

Domínio da função? Então vamos procurar por pontos onde ela não existe, então nosso domínio será todo o R 2 menos esses pontos!

Veja que a expressão no denominador da fração não pode valer 0 , então temos que:

x 2 + y 2 ≠ 0

ou seja, x e y não podem valer 0 ao mesmo tempo! Isso só acontece na origem. Então, nosso domínio fica sendo:

D = { x , y ∈ R 2 | x , y ≠ 0,0 }

E pronto :) parece que esse é o nosso único problema na expressão! Partiu desenhar as curvas de nível!!!

Passo 2

Agora vamos esboçar as curvas. Para isso, é só:

  1. Pegar a função →   F x , y = 10 x 2 - 2 y x 2 + y 2
  2. Colocar o valor do nível no lugar de F x , y .
  3. Ou seja, para a curva em c = 0 , teremos 0 = 10 x 2 - 2 y x 2 + y 2

Agora vamos continuar então os cálculos para c = 0 ?

0 = 10 x 2 - 2 y x 2 + y 2

10 x 2 - 2 y = 0

y = 5 x 2

Beleza! Temos uma parábola no plano O x y , que tem boca no sentido do eixo y .

Passo 3

Agora para c = 1

1 = 10 x 2 - 2 y x 2 + y 2

x 2 + y 2 = 10 x 2 - 2 y

- 9 x 2 + y 2 + 2 y = 0

Completando o quadrado para o y teremos:

- 9 x 2 + y 2 + 2 y + 1 - 1 = 0

y + 1 2 - 9 x 2 = 1

y + 1 2 - x 2 1 9 = 1

Que representa uma hipérbole, com bocas apontadas na direção do eixo y (pois é o eixo da variável que tá com o + na frente), onde vão ficar os vértices?

A hipérbole tem a seguinte equação geral

y - y 0 2 a 2 - x - x 0 2 b 2 = 1

Os vértices vão ser 0 , y 0 + a e 0 , y 0 - a

Nessa hipérbole que temos agora os vértices vão ser 0 , - 1 + 1 e 0 , - 1 - 1 , ou seja, 0,0 e 0 , - 2

Passo 4

Finalmente, para c = 10 temos:

10 = 10 x 2 - 2 y x 2 + y 2

10 x 2 + y 2 = 10 x 2 - 2 y

10 x 2 + 10 y 2 = 10 x 2 - 2 y

10 y 2 + 2 y = 0

Colocando o y em evidência, fica:

y 10 y + 2 = 0

E temos duas retas, uma y = 0 e outra y = - 1 5 , que podem ser entendidas como as raízes da equação acima

Só pra você agradecer por estarmos desenhando apenas as curvas de nível, se liga na função:

Resposta

Em preto, a parábola y = 5 x 2 (curva de nível 0 ), em vermelho, a hipérbole y + 1 2 - x 2 1 9 = 1 (curva de nível 1 ), em azul, a reta y = 0 , e em verde, a reta y = - 1 5 :

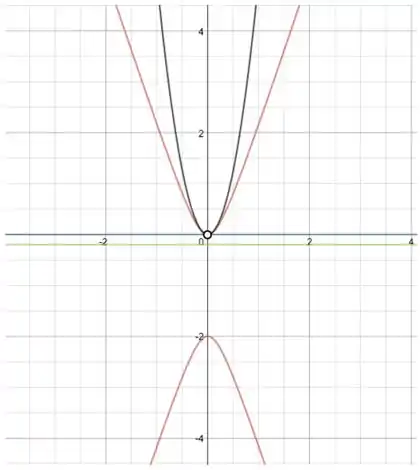
Não esquece de tirar a origem dessas curvas de nível hein!!! Ela não está no domínio.