Determine o domínio da função dada e represente-o graficamente. Esboce duas curvas de nível para cada função.
Passo 1
Olá pessoal, como vocês estão?
Nessa questão recebemos a função de três variáveis dada por:
Sobre essa função precisamos determinar o seu domínio e representar o conjunto desse domínio graficamente. Além disso, também precisamos esboçar duas curvas de nível dessa função.
Beleza?!
Tá, mas vamos com calma em cada uma dessas coisas. Primeiramente, vocês lembram o que é o domínio?
Então, nada mais é do que o conjunto de pontos que podem servir de entrada na nossa função sem que a gente tenha algum absurdo matemático. Ou seja, na prática precisamos verificar os pontos que são restrição na nossa função.
Já as curvas de nível, aqui na verdade teremos superfícies de nível, pois temos uma função de variáveis. Podemos calcular igualando a função a uma constante, tipo assim:
Daí, o enunciado nos pede para colocar dois valores pra essa constante e esboçar a superfície formada.
Show de bola! Vamos começar analisando se tem alguma restrição no domínio da nossa função e depois esboçamos o conjunto e as superfícies de nível!
Vem comigo 😊
Passo 2
Bom, temos a função:
A única restrição nessa função é a raiz quadrada, pois sempre precisamos ter o radicando maior ou igual a zero. Assim:
Ou seja, o nosso domínio é externo à esfera centrada em e com raio igual a . Na prática, significa que o nosso conjunto do domínio é todo o espaço do exceto pela região interna à esfera citada.
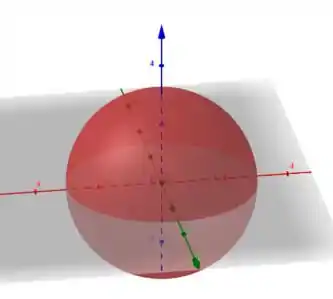
Muito bom!
Passo 3
Indo agora para as superfícies de nível, basta fazermos:
Como queremos esboçar duas superfícies de nível, podemos começar fazendo . Assim:
Ou seja, a nossa primeira superfície de nível é a própria superfície da esfera centrada em e raio .
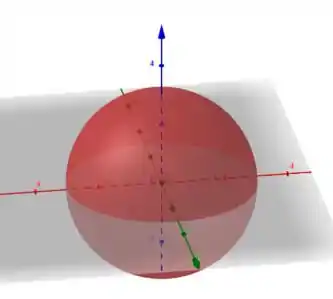
“Ue, mas não vimos que o domínio não inclui essa esfera. Se a esfera não está inclusa no domínio como podemos tê-la como uma superfície de nível?”
Então, de fato se o domínio não inclui uma região não pode ter nenhuma superfície de nível passando por ela.
Porém, aqui nesse caso, o domínio não inclui a região interna à esfera e aqui temos a superfície da esfera. Ou seja, tá tudo certinho, beleza?
Vamos agora tomar . Daí:
Logo, também se trata da superfície de uma esfera, centrada em mas com raio . Tranquilo?
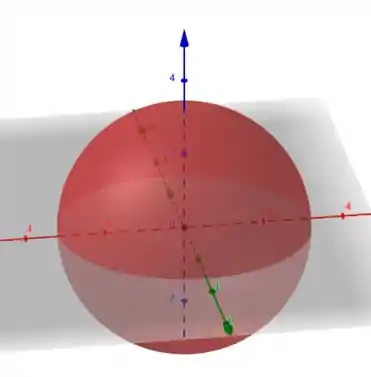
É isso pessoal! Curtiram a solução? Responde AÍ!
Valeeuu!!
Resposta
Resposta no texto.