UERJ, Sem Campus, Cálculo II, Listas de C2 - Profº Ditter Adolfo - 1ª Lista, Questão 6c
6) Esboce o gráfico das funções abaixo (onde ):
(c)
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema queremos esboçar o gráfico da superfície formada pela equação .
Parece complicado? 😐
Para esboçar uma superfície que não conseguimos visualizar logo de cara como é seu comportamento, podemos usar algumas técnicas para nos ajudar.
Como por exemplo podemos encontrar curvas de níveis ou intersecç��es da superfície com um plano, assim, desenhando a curva formada no plano de intersecção podemos obter algo parecido com algumas estruturas da superfície e portanto, ter uma ideia de como é o gráfico de .
Sacou? Bora começar! 😎
Passo 2
A superfície que vamos esboçar é dada por
Fazendo , sendo o nível das curvas de níveis, temos
A partir dessa equação podemos perceber que as curvas de níveis serão circunferências com raio .
Por exemplo em
E também em
Agora voltando para a primeira equação e fixando , vamos obter a intersecção entre a superfície e o plano
Fazendo o mesmo agora para
Tranquilo até aqui? 😐
Passo 3
Esboçando cada curva em seus devidos planos e níveis, vamos obter
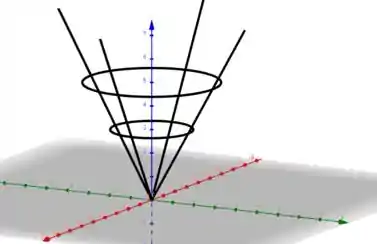
Dessa forma, podemos ter uma ideia de como a superfície se comporta no espaço.
A partir das curvas, podemos imaginar que a superfície se pareça com um cone de cabeça para baixo, ou seja
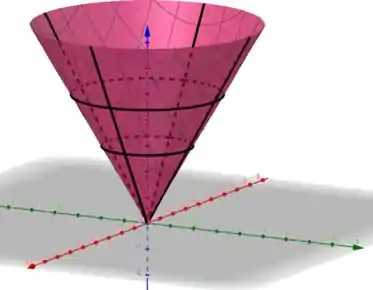
Sacou como faz? Responde Aí! 😉
Resposta
