Descreva e esboce as curvas de nível e o gráfico da função:
Passo 1
Ooii pessoal, tudo bem com vocês?
Nessa questão recebemos a função de duas variáveis dada por:
E, precisamos determinar a curva de nível dessa função, bem como o seu gráfico.
Pra determinar a curva de nível basta igualarmos a função dada a uma constante. A partir disso, analisamos a curva que será formada no plano.
Já para determinar o gráfico da função de duas variáveis, precisamos analisar a figura tridimensional que a nossa lei de função irá gerar.
Vem com a gente que esses passos vão ficar super claros 😊
Passo 2
Começando pela curva de nível, precisamos igualar a expressão da lei de formação a uma constante.
Assim:
Aplicando o logaritmo natural em ambos os lados, temos:
Como também é uma constante, escrevemos que:
onde
Isso é a equação de uma circunferência centrada em cujo raio vale .
Logo, podemos esboçá-la como:
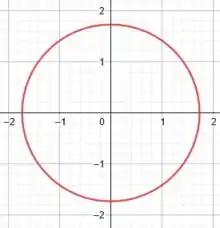
Perfeito!
Passo 3
Agora que já desenhamos a curva de nível, vamos pensar no gráfico da função.
A nossa função é dada por:
Conforme o termo cresce, menor fica a nossa função .
O máximo valor que a função assume é justamente quando:
Quando , temos .
De modo que todo o plano é coberto.
Portanto, podemos esboçar o seu gráfico como:
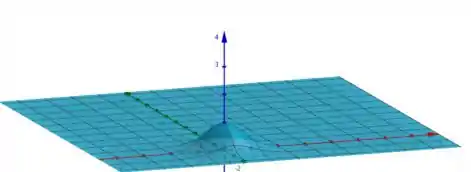
Diferente né? Mas é issoo!
Espero que vocês tenham entendido bem direitinho, até a próxima 😊
Resposta
Resposta no texto.