UERJ, Sem Campus, Cálculo II, Listas de C2 - Profº Ditter Adolfo - 1ª Lista, Questão 6d
6) Esboce o gráfico das funções abaixo (onde ):
(d)
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema queremos esboçar o gráfico da superfície formada pela equação .
Parece complicado? 😐
Para esboçar uma superfície que não conseguimos visualizar logo de cara como é seu comportamento, podemos usar algumas técnicas para nos ajudar.
Como por exemplo podemos encontrar curvas de níveis ou intersecções da superfície com um plano, assim, desenhando a curva formada no plano de intersecção podemos obter algo parecido com algumas estruturas da superfície e portanto, ter uma ideia de como é o gráfico de .
Sacou? Bora começar! 😎
Passo 2
A superfície que vamos esboçar é dada por
Fazendo , sendo o nível das curvas de níveis, temos
Assim podemos perceber que as curvas de níveis da superfície serão circunferências de raio .
Por exemplo em
E também em
Agora esboçando a intersecção da superfície com o plano , temos
Fazendo o mesmo para o plano
Bacana, não é? 😉
Passo 3
Esboçando cada curva em seu devido nível ou plano, chegamos em
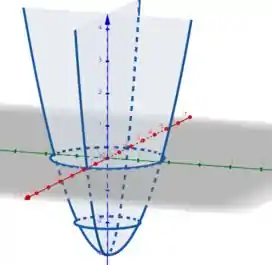
A partir daí podemos imaginar o comportamento da superfície no espaço.
Além disso, nesse caso podemos perceber que nossa superfície é um paraboloide dado por
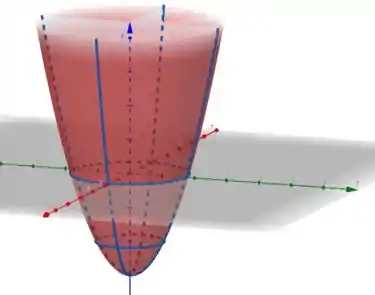
O que achou? Foi de boa? Responde aí! 😊
Resposta
