UFF, Sem Campus, Cálculo IIB, 2ª VE - Prof. Sérgio Almaraz - 2014.2, Questão 3a.
3 - Considere a função e a região .
(a) Esboce em um único desenho a região e as curvas de nível de .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, estamos interessados em obter a região e as curvas de níveis de em .
E aí, como podemos fazer isso? 😁
Curvas de nível são uma maneira de visualizar graficamente as soluções de uma função com duas variáveis. São linhas que conectam pontos na superfície de uma função que possuem o mesmo valor da função. Em outras palavras, para uma função , as curvas de nível representam os pontos onde é constante.
Para obter as curvas de nível de uma função , você precisa seguir os seguintes passos:
Escolha alguns valores constantes para , por exemplo, , , ...
Para cada valor constante escolhido, resolva a equação constante para obter uma expressão para a curva de nível correspondente.
E por fim, trace as curvas de nível obtidas em um gráfico 2D com eixos e .
Sacou? Bora começar! 😊
Passo 2
Vamos começar esboçando a região .
Essa região é dada por , ou seja, pela parte de menor que , menor que e para e maiores que .
Para facilitar a visualização, podemos isolar em um lado da desigualdade
Esboçando essas curvas no plano cartesiano, temos que
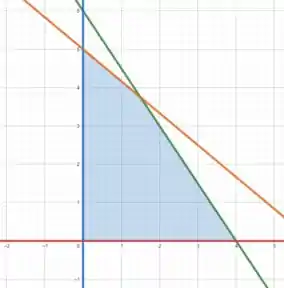
Tranquilo até aqui? 😁
Passo 3
Agora vamos obter as curvas de níveis de que passa em .
Se , igualando a uma constante, temos
Isolando em um lado...
Para descobrir quais valores de podemos usar, vamos fazer e comparar com o intervalo da região em que também é igual a
Como de nossa região varia de a quando , pode ser qualquer valor entre e , ou seja
Escolhendo qualquer valor nesse intervalo, passará pela região .
Legal, né? 😎
Passo 4
Assim, vamos analisar os níveis , , e .
Para
Temos uma reta que passa em quando e em quando
Para
Temos outra reta que passa por quando e quando
Para
Temos uma reta que passa em quando e em quando
E por fim, para
Temos uma reta que passa em quando e em quando
Conseguiu visualizar essas características? 🤔
Passo 5
Assim, esboçando as curvas em cada um dos níveis, vamos obter algo aproximadamente igual a
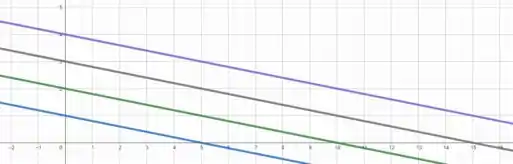
Agora vamos juntar as curvas com a região e esboçar apenas as partes dos níveis que fazem parte da região .
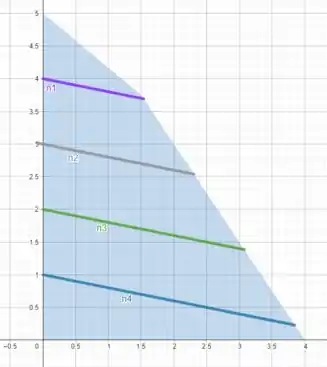
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
