UFPE, Cálculo 2, 1°EE, 2012.2, questão 1
Seja uma função cujo valor do ponto representa a temperatura em neste ponto. Se é dada por:
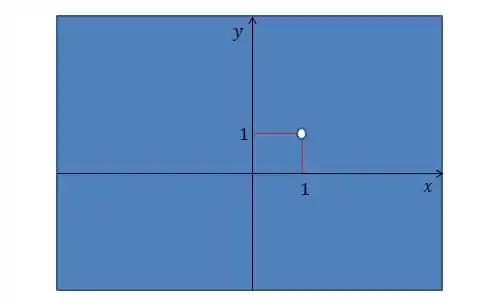
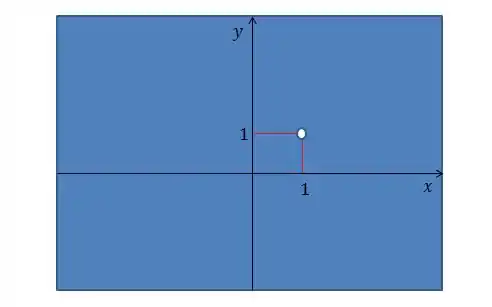
- Determine e esboce graficamente o domínio da função
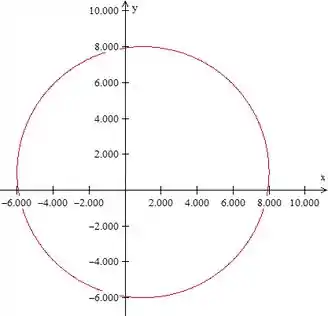
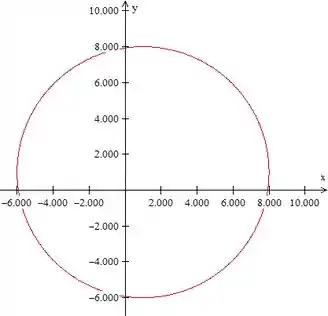
- Esboce a isoterma de temperatura
- Encontre o(s) ponto(s) onde a temperatura seja máxima ao longo da reta
Passo 1
- Vamos começar ajeitando essa função. Temos:
- Substituindo , temos:
- Bom, primeiramente repare que a reta , está no domínio da função, pois não compreende o ponto . Visto isso, basta substituir na função. Vai ficar:
Passo 2
O denominador tem de ser diferente de zero, logo:
Então, o domínio será:
Ou seja, todo menos o ponto
Passo 3
Graficamente:
Passo 4
Então fica:
Essa é a equação de uma circunferência de raio , com centro em .
Graficamente:
Passo 5
Passo 2
Temos uma função de apenas uma variável. Para encontrar seus valores máximos e mínimos vamos derivar essa função e igualar a zero. Fica:
Logo, temos
Passo 3
Fazendo o teste da derivada segunda nesse ponto:
Logo, como a segunda derivada é menor do qe zero, o ponto é de máximo.
Logo, o ponto onde a temperatura é máximo é
Resposta
