UERJ, Sem Campus, Cálculo II, Listas de C2 - Profª Gabriela Coutinho - Lista 4, Questão 3b
Considere a função .
b) Desenhe as curvas de nível de , para os níveis , e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente desenhar as curvas de nível de , para os níveis , e .
As curvas de nível nada mais são do que a interseção do gráfico com um plano (onde é uma constante). Na prática, é só igualar a função a constante dada. Depois disso, plotamos a curva no espaço cartesiano.
Vamos lá!
Passo 2
Vamos começar encontrando a curva de nível para . Igualando a nossa função , temos:
Que é apenas um plano no espaço tridimensional. Plotando esse plano (em vermelho) junto com a nossa função (em azul), temos:
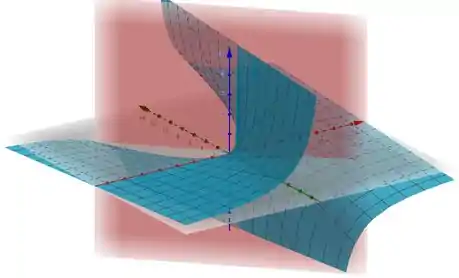
Passo 3
Agora vamos repetir o processo para . Teremos:
Que também é um plano no espaço tridimensional, como mostrado em vermelho no gráfico:
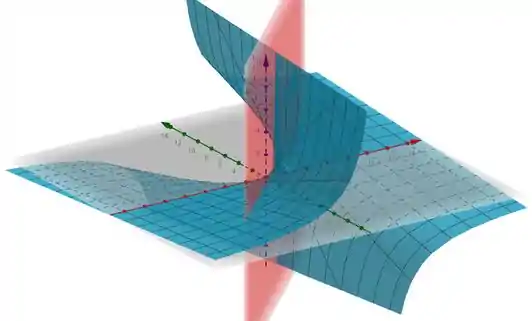
Passo 4
Por fim, para , teremos:
Plotando esse plano mais uma vez, temos:
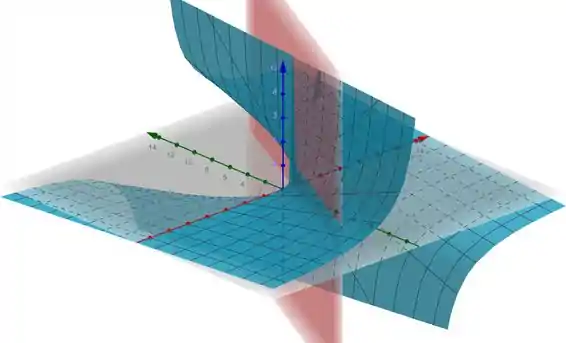
Prontinho, galera! Até a próxima! 😉