UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille - Segunda Lista de Exercícios, Questão 22g
Descreva e esboce as curvas de nível e o gráfico da função:
Passo 1
E aí gente, tudo beleza?
Nessa questão recebemos a função de duas variáveis dada por:
E, precisamos determinar a curva de nível dessa função, bem como o seu gráfico.
Pra determinar a curva de nível basta igualarmos a função dada a uma constante. A partir disso, analisamos a curva que será formada no plano.
Já para determinar o gráfico da função de duas variáveis, precisamos analisar a figura tridimensional que a nossa lei de função irá gerar.
Vem com a gente que esses passos vão ficar super claros 😊
Passo 2
Começando pela curva de nível, precisamos igualar a expressão da lei de formação a uma constante.
Assim:
Daí, elevando ao quadrado em ambos lados, vamos ter:
Logo:
Essa é justamente a equação de uma circunferência, centrada em e com raio valendo:
Assim, podemos esboçar a curva de nível da função:
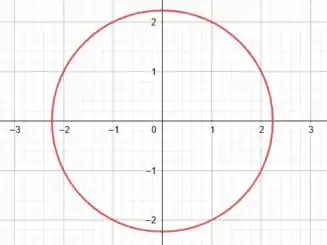
(onde ).
Perfeito!
Passo 3
Agora que já desenhamos a curva de nível, vamos pensar no gráfico da função.
Como já sabemos que a curva de nível é uma circunferência, podemos imaginar que o gráfico da função é formado pela superposição dessas curvas de nível, onde cada uma delas tem o valor da constante um pouco maior.
Além disso, quando:
A função vale . Ou seja, estamos no pano . E, abaixo disso a função não existe pela restrição da raiz quadrada na lei de formação.
Logo, temos:
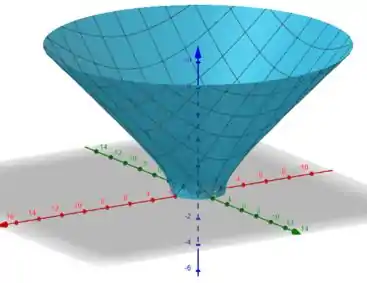
Aee! Finalizamos 😊
Até a próxima!
Resposta
Resposta no texto.