Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Curvas de Nível

Ver Teoria
Exercício 351234567891011121314151617181920212223242526272829303132333436373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.7a

1.7. Seja f x , y = 2 x 2 + 4 y 2 x 2 + y 2 + 1 .

a. Esboce as curvas de nível de f dos níveis c = 1 , c = 2 e c = 3

Passo 1

E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!

Nesse problema queremos obter as curvas de níveis da função f x , y = 2 x 2 + 4 y 2 x 2 + y 2 + 1 para os níveis c = 1 , c = 2 e c = 3 .

E agora? O que temos que fazer? 🤔

Para obter as curvas de níveis de uma função, temos que fazer f x , y = c onde c representa o nível que queremos representar.

Dessa forma, manipulando a equação resultante, vamos obter uma equação conhecida ou uma função bidimensional.

Tranquilo? Bora lá! 😁

Passo 2

Vamos começar fazendo f x , y = c

f x , y = 2 x 2 + 4 y 2 x 2 + y 2 + 1 = c

2 x 2 + 4 y 2 = c x 2 + y 2 + 1

Simplificando um pouquinho

2 x 2 + 4 y 2 = c x 2 + c y 2 + c

2 x 2 - c x 2 + 4 y 2 - c y 2 = c

2 - c x 2 + 4 - c y 2 = c

2 - c x 2 c + 4 - c y 2 c = 1

x 2 c 2 - c + y 2 c 4 - c = 1

Pela estrutura dessa equação, vemos que se trata de uma estrutura cônica.

Bacana, não é? 😉

Passo 3

Para c = 1 temos

x 2 1 2 - 1 + y 2 1 4 - 1 = 1

x 2 + y 2 1 3 = 1

Para c = 2

x 2 2 2 - 2 + y 2 2 4 - 2 = 1 → x 2 2 0 + y 2 2 2 = 1

y 2 = 1

y = ± 1

E para c = 3

x 2 3 2 - 3 + y 2 3 4 - 3 = 1 → x 2 - 3 1 + y 2 3 1 = 1

- x 2 3 + y 2 3 = 1

Esboçando essas curvas no plano x y , temos

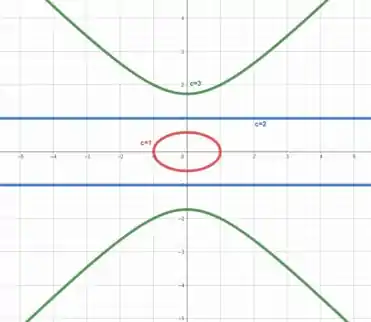
O que achou? Foi de boa? Responde aí! 😊

Resposta

c = 1 → x 2 + y 2 1 3 = 1

c = 2 → y = ± 1

c = 3 → - x 2 3 + y 2 3 = 1