UFMG – Cálculo 2 – 2022/2 – Lista de exercícios 7
1.6) Faça os mapas de contornos das funções a seguir, mostrando várias curvas de nível.
a)
b)
c)
d)
Passo 1
Falaa... tudo bem??
Nessa questão vamos fazer o mapa de contorno da função, mostrando algumas curva de nível.
Pra isso vamos lembrar que pra fazer curvas de nível igualamos a função a uma constante .
Depois variamos essa constante e fazemos o mapa de contorno.
Passo 2
Igualando a :
Isolando
Temos retas de inclinação
Fazendo algumas curvas de nível. Para e 3:
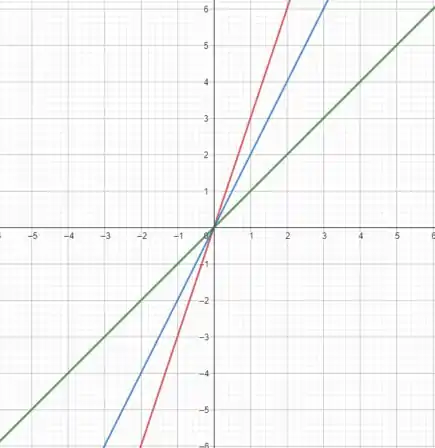
Resposta
Resposta nos passos.