Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Curvas de Nível

Ver Teoria
Exercício 341234567891011121314151617181920212223242526272829303132333536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.2c

1.2. Esboce uma família de curvas de nível das seguintes funções:

c) f x , y = x 2 x 2 - y 2

Passo 1

Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nosso objetivo nessa questão é esboçar algumas curvas de níveis da função f x , y = x 2 x 2 - y 2 .

E aí, como fazemos isso? 🤔

Para esboçar uma curva de nível podemos imaginar que uma curva de nível é o gráfico formado pela intersecção de f com um plano z = k , em que k representa o nível (a altura) com relação ao plano x y .

Na prática, temos que fazer f x , y = k e assim determinar valores para k para obter funções bidimensionais.

Vamos ver como é isso! 😉

Passo 2

Fazendo f x , y = k , temos

f x , y = x 2 x 2 - y 2 = k

Vamos tentar isolar y em um lado da igualdade

x 2 = k x 2 - y 2

x 2 = k x 2 - k y 2

k y 2 = k x 2 - x 2

k y 2 = x 2 k - 1

Simplificando um pouco mais

y 2 = x 2 k - 1 k

y = ± x 2 k - 1 k

Agora temos que determinar alguns níveis de k para esboçar suas curvas.

Tranquilo até aqui? 😉

Passo 3

Podemos obter as curvas dos níveis k = - 1 , k = 1 e de k = 2

Começando por k = - 1 , temos

y = ± x 2 - 1 - 1 - 1 = ± - 2 x 2 - 1

y = ± 2 x 2

y = ± 2 x

Para k = 1

y = ± x 2 1 - 1 1 = ± x 2 0 1

y = 0

Para k = 2

y = ± x 2 2 - 1 2 = ± x 2 2

y = ± x 2

Esboçando essas curvas no plano x y , temos

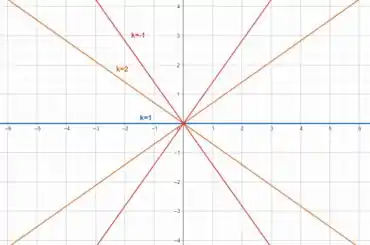
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

y = ± x 2 k - 1 k