A temperatura em um ponto de uma placa de metal plana é graus.
- Encontre a temperatura no ponto .
- Encontre a equação da curva ao longo da qual a temperatura tem um valor constante e igual a graus.
- Esboce a curva do item (b).
Passo 1
Resolvendo o item (a):
Basta substituir e para descobrir :
Passo 2
Resolvendo o item (b):
Queremos encontrar a curva em que a temperatura é constante e igual a . Logo:
Dividindo os dois lados por :
Portanto, os pontos que satisfazem essa equação satisfazem .
Observação: note que esses pontos são uma curva de nível da função !
Passo 3
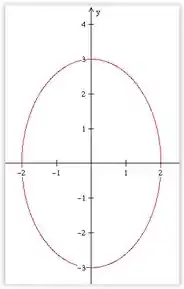
Perceba que equação da curva que acabamos de encontrar é uma elipse.
Portanto, seu gráfico é o seguinte:
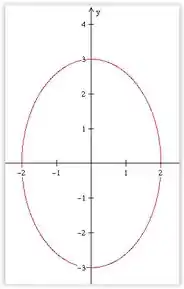
Resposta