UFSC, Joinville, Cálculo II, P2 - 2022.2, Questão 2b
2. Considere a função .
b) Esboce a curva de nível de que passa pelo ponto .
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema queremos obter a curva de nível que corta a função no ponto .
Tem ideia de como fazer isso? 🤔
a curva de nível de uma função é uma curva que é formada ao se cortar a superfície da função em um determinado nível em .
Portanto a primeira coisa que temos que fazer é descobrir qual é o nível que contêm o ponto da função .
Depois igualamos a função a uma variável e definimos uma curva bidimensional a partir da equação resultante.
Sacou? Bora começar! 😉
Passo 2
Vamos começar substituindo o ponto em para saber qual nível de pertence o ponto...
Ou seja, queremos esboçar o nível de ...
Igualando a , temos
Fazendo
Elevando os dois lados a para simplificar a equação
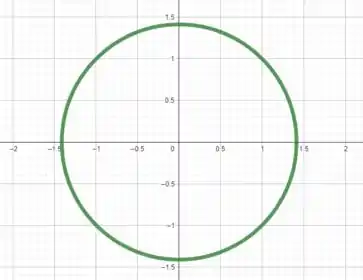
Esboçando a circunferência de raio centrada na origem, temos
O que achou? Foi de boa? Responde aí! 😊