UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Marcos André - 1ª Lista de Exercícios, Questão 1e
Determine o domínio da função dada e represente-o graficamente. Esboce duas curvas de nível para cada função.
Passo 1
Eaí galera, como vocês estão?
Nessa questão recebemos a função de três variáveis dada por:
Sobre essa função precisamos determinar o seu domínio e representar o conjunto desse domínio graficamente. Além disso, também precisamos esboçar duas curvas de nível dessa função.
Beleza?!
Tá, mas vamos com calma em cada uma dessas coisas. Primeiramente, vocês lembram o que é o domínio?
Então, nada mais é do que o conjunto de pontos que podem servir de entrada na nossa função sem que a gente tenha algum absurdo matemático. Ou seja, na prática precisamos verificar os pontos que são restrição na nossa função.
Já as curvas de nível, aqui na verdade teremos superfícies de nível, pois temos uma função de variáveis. Podemos calcular igualando a função a uma constante, tipo assim:
Daí, o enunciado nos pede para colocar dois valores pra essa constante e esboçar a superfície formada.
Show de bola! Vamos começar analisando se tem alguma restrição no domínio da nossa função e depois esboçamos o conjunto e as superfícies de nível!
Vem comigo 😊
Passo 2
Começando pelo domínio, temos a função:
Como trata-se de uma fração, a única restrição que vamos ter é o denominador diferente de zero. Assim:
Assim, o conjunto de pontos que não podem pertencer ao domínio da nossa função, s��o os pontos do tipo:
Ou seja, o plano dado por:
Assim, o nosso domínio de , vale:
O esboço desse domínio é basicamente todo o exceto pelo plano citado. Ou seja:
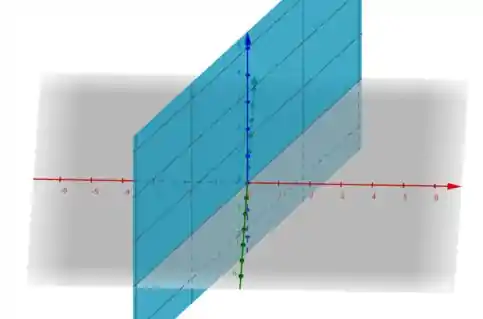
Ou seja, todo o espaço menos o plano em azul.
Passo 3
Por fim, vamos analisar as superfícies de nível dessa função. Temos:
Daí, precisamos escolher dois valores para .
Para , temos:
O que nos dá a seguinte superfície de nível:
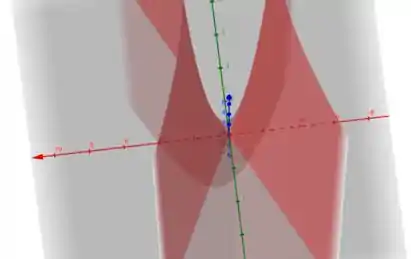
E, fazendo , vamos ter:
Esboçando a superfície de nível dessa equação, temos:
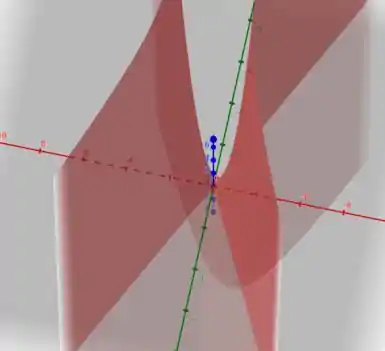
Que nos dá uma superfície de nível bem parecida com a anterior.
E é isso gente, conseguiram entender bem? Responde Aí!
Até a próxima 😊
Resposta
Resposta no texto.