UFSC, Joinvile, Cálculo II, Provas Profº Rómulo Castillo - P2 2015.1, Questão 1c
Dada
c) Esboce o e a curva de nível .
Passo 1
Eaew, belezinha?
A questão pede para a gente calcular o gradiente da função f(x,y) no ponto (1,1) e a curva de nível para f(x,y) =1. Primeiro, vamos dar uma olhada na superfície definida por f(x,y): temos que para planos de y constante e positivo, as curvas f(x) são parábolas com concavidade positiva, enquanto que, para planos de y constante e negativo, as curvas são parábolas com concavidade negativa, como vemos nos esboços abaixo, onde os eixos x, y e z estão representados, respectivamente, em vermelho, verde e azul:
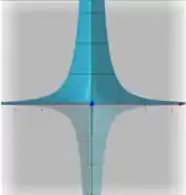
Da segunda imagem (que representa a vista do plano xy a partir do eixo z), vemos que as curvas de f(x,y) constante são da forma
Em particular, para f(x,y) = 1, temos que a função y(x) é dada por
Essa função vai rapidamente à zero para valores de x grandes, devido ao denominador e, similarmente, cresce rapidamente conforme nos aproximamos de x = 0. Devido ao termo quadrático, temos que a função é simétrica em relação ao eixo x, de modo que é sempre positiva, como esboçado na figura a seguir:
Agora, só precisamos calcular o gradiente da função no ponto (1,1). Para isso vamos precisar calcular as derivadas parciais da função. Então vamos lá derivar!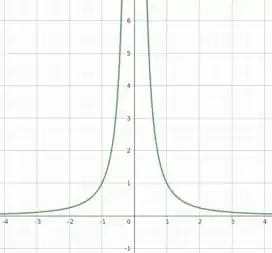
Passo 2
Para obter o gradiente no ponto (1,1), precisamos derivar a função de duas variáveis. Para isso, consideramos a variável y como constante e derivamos em relação à x. Então, temos que:
No ponto (1,1), essa expressão é igual à 2. Agora fazemos a mesma coisa para y, dessa vez considerando x como constante:
Em (1,1), a expressão acima assume o valor 1. Então, como o gradiente de uma função é dado por , temos que
Graficamente, temos no ponto (1,1) da curva um vetor que é perpendicular à curva tangente nesse ponto, como esperado, visto que o gradiente é sempre perpendicular às curvas de nível. A figura a seguir ilustra a curva de nível f(x,y) = 1 e o vetor gradiente no ponto (1,1):
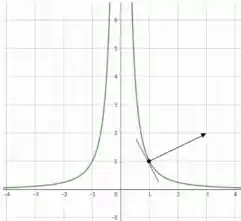
Resposta
Ao decorrer da questão.