Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Curvas de Nível

Ver Teoria
Exercício 321234567891011121314151617181920212223242526272829303133343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

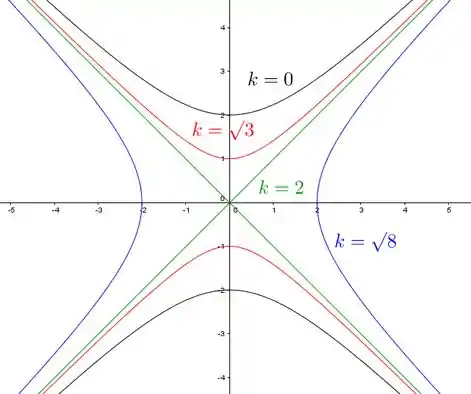
Seja f x , y = x 2 - y 2 + 4 . Determine equações para as curvas de nível k de f para k = 0 ,   k = 3 ,   k = 2 e k = 8 . Faça o esboço dessas curvas.

Passo 1

Vamos ver como fica a equação de uma curva de nível k qualquer:

f x , y = k

x 2 - y 2 + 4 = k

x 2 - y 2 + 4 = k 2

Ou seja:

x 2 - y 2 = k 2 - 4

Passo 2

Beleza, vamos começar pela curva de nível k = 0 :

x 2 - y 2 = 0 - 4 = - 4

Dividindo tudo por - 4 :

- x 2 4 + y 2 4 = 1

y 2 2 - x 2 2 = 1

Reconhecemos a equação de uma hipérbole.

Passo 3

Pra k = 3 :

x 2 - y 2 = 3 - 4 = - 1

Dividindo tudo por - 1 , obtemos

y 2 - x 2 = 1 ,

que também é a equação de uma hipérbole.

Passo 4

Pra k = 2 :

x 2 - y 2 = 4 - 4 = 0

y 2 = x 2

y = ± x

Ou seja, nesse caso temos duas retas: y = x e y = - x .

Passo 5

Pra finalizar, k = 8 :

x 2 - y 2 = 8 - 4 = 4

x 2 4 - y 2 4 = 1

x 2 2 - y 2 2 = 1

Que é mais uma equação de hipérbole!

Passo 6

Agora chegou a hora de esboçar essas marotas...

Tem duas retas bem tranquilas, mas não tem jeito, tem que saber esboçar hipérbole! Enfim, essas curvas de nível vão ficar assim:

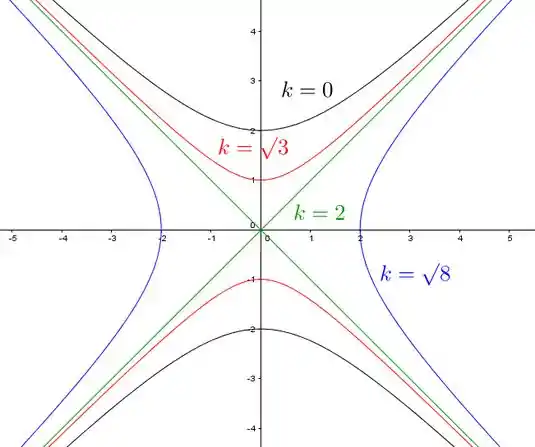
Resposta

k = 0 →     y 2 2 - x 2 2 = 1

k = 3 →     y 2 - x 2 = 1

k = 2 →     y = x   e   y = - x

k = 8 →     x 2 2 - y 2 2 = 1

Esboço: