UERJ, Sem Campus, Cálculo II, Listas de C2 - Profº Ditter Adolfo - 1ª Lista, Questão 2a
2) Representar no plano cartesiano as curvas de nível das funções abaixo correspondentes aos valores de nível dados
(a) , , , , .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, temos que calcular e esboçar no plano cartesiano as curvas de níveis solicitadas da função .
Tem ideia de como fazemos isso? 😬
Para esboçar a curva de nível de uma função, temos que igualar a , onde representa a curva de nível que vamos substituir.
Na prática, temos uma função tridimensional e é o plano paralelo ao plano de altura em . Esse plano corta a função em algum momento e esse corte gera uma curva bidimensional, sendo essa curva nossa curva de nível!
Sacou? Bora começar! 😎
Passo 2
A função foi dada como
E os níveis que vamos obter são , , e .
Igualando , temos
Isolando em um lado da igualdade, vamos conseguir escrever em função de
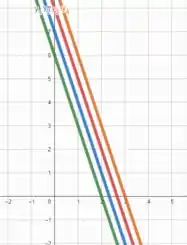
Como é uma constante, podemos ver que as curvas de níveis de serão retas de coeficiente angular e coeficiente linear .
Para
Para
Para
E para
Esboçando essas retas no plano cartesiano, vamos obter
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
