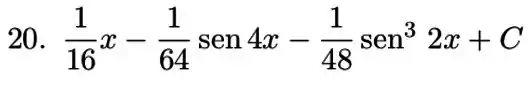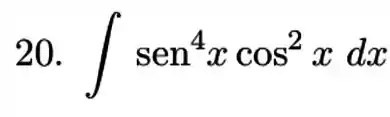
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 115123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Para começar esse exercício, vamos fazer uma substituição trigonométrica

cos 2 ⁡ x = 1 - s e n 2 x

Então nossa integral vai ficar

∫ s e n 4 x cos 2 ⁡ x d x = ∫ s e x 4 x 1 - s e n 2 x d x

∫ s e n 4 x cos 2 ⁡ x d x = ∫ s e n 4 x   d x - ∫ s e n 6 x   d x

Passo 2

Lá vamos nós para mais uma substituição, sabemos que

s e n 2 x = 1 - cos ⁡ 2 x 2

Aplicando na nossa integral

∫ s e n 4 x cos 2 ⁡ x d x = ∫ 1 - cos ⁡ 2 x 2 2   d x - ∫ 1 - cos ⁡ 2 x 2 3   d x

Expandindo essas expressões ficamos com

∫ s e n 4 x cos 2 ⁡ x d x = ∫ 1 - 2 cos ⁡ 2 x + cos 2 ⁡ 2 x 4 d x - ∫ 1 - 3 cos ⁡ 2 x + 3 cos 2 ⁡ 2 x - cos 3 ⁡ 2 x 8 d x  

E se formos resolvendo aos poucos as integrais, chegaremos em

∫ s e n 4 x cos 2 ⁡ x d x = 1 4 x - 2 1 2 s e n 2 x + ∫ cos 2 ⁡ 2 x d x - 1 8 x - 3 1 2 s e n 2 x + 3 ∫ cos 2 ⁡ 2 x d x - ∫ cos 3 ⁡ 2 x d x

Passo 3

Primeiro vamos resolver a integral

∫ cos 2 ⁡ 2 x d x

cos 2 ⁡ ( 2 x ) = 1 + cos ⁡ 4 x 2  

Então

∫ cos 2 ⁡ 2 x d x = ∫ 1 + cos ⁡ 4 x 2 d x

∫ cos 2 ⁡ 2 x d x = 1 2 x + 1 8 s e n ( 4 x )

Passo 4

Vamos resolver a integral

∫ cos 3 ⁡ 2 x d x = ∫ cos 2 ⁡ 2 x cos ⁡ ( 2 x ) d x

Vamos substituir cos 2 ⁡ 2 x = 1 - s e n 2 2 x

∫ cos 3 ⁡ 2 x d x = ∫ ( 1 - s e n 2 2 x )   c o s ⁡   ( 2 x )   d x

E vamos resolver por substituição

u = s e n 2 x

d u = 2 c o s ⁡ ( 2 x ) d x

∫ cos 3 ⁡ 2 x d x = 1 2 ∫ 1 - u 2 d u

∫ cos 3 ⁡ 2 x d x = 1 2 u - u 3 3

Desfazendo a substituição

∫ cos 3 ⁡ 2 x d x = 1 2 s e n   2 x - s e n 3 2 x 3

Passo 5

Agora só falta substituir lá na nossa expressão

∫ s e n 4 x cos 2 ⁡ x d x = 1 4 x - 2 1 2 s e n 2 x + ∫ cos 2 ⁡ 2 x d x - 1 8 x - 3 1 2 s e n 2 x + 3 ∫ cos 2 ⁡ 2 x d x - ∫ cos 3 ⁡ 2 x d x

∫ cos 2 ⁡ 2 x d x = 1 2 x + 1 8 s e n ( 4 x )

∫ cos 3 ⁡ 2 x d x = 1 2 s e n   2 x - s e n 3 2 x 3

∫ s e n 4 x cos 2 ⁡ x d x = 1 4 x - s e n 2 x + 1 2 x + 1 8 s e n ( 4 x ) - 1 8 x - 3 2 s e n 2 x + 3 2 x + 3 8 s e n ( 4 x ) - 1 2 s e n 2 x + 1 6 s e n 3 2 x

∫ s e n 4 x cos 2 ⁡ x d x = 1 16 - 1 64 s e n 4 x - 1 48 s e n 3 2 x + C

Prontinho!

Resposta

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x