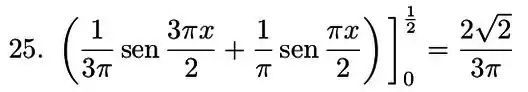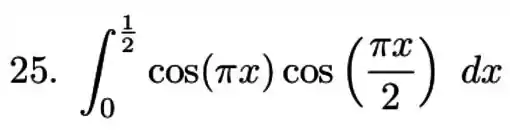
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 149123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Vamos lá! Precisamos de uma forma melhor de escrever

cos ⁡ ( π x ) cos ⁡ π x 2  

E como vamos fazer isso? Fica calmo! Segura na minha mão e vamos lembrar lá do ensino médio, você lembra que

cos ⁡ a + b = cos ⁡ a cos ⁡ b - sen ⁡ a sen ⁡ b

cos ⁡ a - b = cos ⁡ a cos ⁡ b + sen ⁡ a sen ⁡ b

Lembrou? Então, se somarmos essas equações teremos

cos ⁡ a + b + cos ⁡ ( a - b ) = 2 cos ⁡ a cos ⁡ b

cos ⁡ a cos ⁡ b = 1 2 cos ⁡ a + b + 1 2 cos ⁡ ( a - b )

Olha só! Isso parece com o nosso problema

a = π x

b = π x 2

Então

cos ⁡ π x cos ⁡ π x 2 = 1 2 cos ⁡ π x + π x 2 + 1 2 cos ⁡ π x - π x 2

cos ⁡ π x cos ⁡ π x 2 = 1 2 cos ⁡ 3 π x 2 + 1 2 cos ⁡ π x 2

Aplicando isso na nossa integral vamos ficar com

∫ 0 1 / 2 cos ⁡ π x cos ⁡ π x 2   d x = ∫ 0 1 / 2 1 2 cos ⁡ 3 π x 2 + 1 2 cos ⁡ π x 2 d x

∫ 0 1 / 2 cos ⁡ π x cos ⁡ π x 2   d x = ∫ 0 1 / 2 1 2 cos ⁡ 3 π x 2 d x + ∫ 0 1 / 2 1 2 cos ⁡ π x 2 d x

Passo 2

Agora que a gente reescreveu, fica bem mais fácil de resolver nossas integrais. Vamos fazer isso pelo método da substituição. Para o caso da integral

∫ 0 1 / 2 1 2 cos ⁡ 3 π x 2 d x = 1 2 ∫ 0 1 / 2 cos ⁡ 3 π x 2 d x

Se aplicarmos

u = 3 π x 2

d u = 3 π 2 d x

2 d u 3 π = d x

1 2 ∫ 0 1 / 2 cos ⁡ 3 π x 2 d x = 1 2 2 3 π ∫ 0 1 / 2 cos ⁡ u d u

1 2 ∫ 0 1 / 2 cos ⁡ 3 π x 2 d x = 1 3 π sen ⁡ u 0 1 / 2

Então

∫ 0 1 / 2 cos ⁡ π x cos ⁡ π x 2   d x = 1 3 π sen ⁡ u 0 1 / 2 + ∫ 0 1 / 2 1 2 cos ⁡ π x 2 d x

Refazendo a substituição

∫ 0 1 / 2 cos ⁡ π x cos ⁡ π x 2   d x = 1 3 π sen ⁡ 3 π 2 0 1 / 2 + ∫ 0 1 / 2 1 2 cos ⁡ π x 2 d x

Se fizermos o mesmo para a segunda integral, vamos ficar com

∫ 0 1 / 2 cos ⁡ π x cos ⁡ π x 2   d x = 1 3 π sen ⁡ 3 π x 2 0 1 / 2 + 1 π sen ⁡ π x 2 0 1 / 2

Passo 3

Agora só falta aplicar os limites de integração

∫ 0 1 / 2 cos ⁡ π x cos ⁡ π x 2   d x = 1 3 π sen ⁡ 3 π x 2 0 1 / 2 + 1 π sen ⁡ π x 2 0 1 / 2

∫ 0 1 / 2 cos ⁡ π x cos ⁡ π x 2   d x = 1 3 π sen ⁡ 3 π 4 - 1 3 π sen ⁡ 0 + 1 π sen ⁡ π 4 - 1 π sen ⁡ 0

∫ 0 1 / 2 cos ⁡ π x cos ⁡ π x 2   d x = 1 3 π 2 2 + 1 π 2 2

∫ 0 1 / 2 cos ⁡ π x cos ⁡ π x 2   d x = 2 2 3 π

Resposta

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x