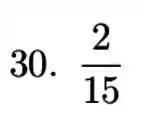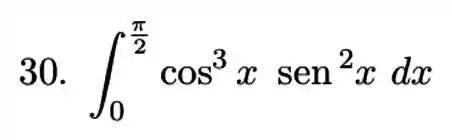
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 127123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Vamos começar! De cara, podemos tentar utilizar a identidade trigonométrica

cos 2 ⁡ x = 1 - sen 2 ⁡ x

Aplicando na nossa integral

∫ cos 3 ⁡ x sen 2 ⁡ x d x = ∫ cos ⁡ x ( 1 - sen 2 ⁡ x ) sen 2 ⁡ x d x

Passo 2

Agora, podemos usar um método da substituição para simplificar nossa integral

u = sen ⁡ x

d u = cos ⁡ x d x  

Substituindo na nossa integral

∫ cos 3 ⁡ x sen 2 ⁡ x d x = ∫ 1 - u 2 u 2 d u

E podemos separar em duas integrais

∫ cos 3 ⁡ x sen 2 ⁡ x d x = ∫ u 2 d u - ∫ u 4 d u

Passo 3

Integrando nossa expressão

∫ cos 3 ⁡ x sen 2 ⁡ x d x = u 3 3 - u 5 5

Desfazendo a substituição

u = sen ⁡ x

∫ cos 3 ⁡ x sen 2 ⁡ x d x = sen 3 ⁡ x 3 - sen 5 ⁡ x 5

Passo 4

Aplicando os limites de integração

∫ 0 π / 2 cos 3 ⁡ x sen 2 ⁡ x d x = sen 3 ⁡ π 2 3 - sen 5 ⁡ π 2 5 - sen 3 ⁡ ( 0 ) 3 + sen 5 ⁡ 0 5

Como sen ⁡ 0 = 0

∫ 0 π / 2 cos 3 ⁡ x sen 2 ⁡ x d x = 1 3 - 1 5 = 2 15

Resposta

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x