UnB – Cálculo 1 – Lista de Exercícios 14 – Questão 6c
Após identificar a técnica apropriada, determine o valor das integrais abaixo
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou te ajudar!
O problema nos deu essa integral aqui
E pediu para resolvermos! Ué, mas por onde começar? Olhando sempre na tabela! Se você logo de cara não identificar uma fórmula que se adeque, então precisamos usar alguma técnica!
Beleza? Como não encontramos nenhuma fórmula da tabela, vamos aos métodos! Começando pelo método da substituição: nele a gente tenta encontrar uma parte do integrando para chamar de e que o restante do integrando tenha a sua derivada
Mas não temos nada isso não é? E agora?
O próximo método que você vai tentar é o: método de integração por partes
Nesse método você vai escolher no integrando uma parte para ser e outra para ser . O método nos diz que a integral de é
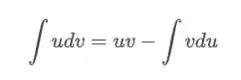A ideia é transformar a integral cabeluda do lado esquerdo, em uma mais simples do lado direito.
E é esse método que vamos aplicar aqui! (os outros falam sobre integrandos com produto de trigonométricas e de razão e polinômios, então é esse por partes mesmo que vamos usar!) Mas relaxa, vou fazer passo a passo com você!
Vamos começar?
Passo 2
Agora nossa missão é integrar essa coisa!
Como vimos nessa lista, integrais que tem como integrando o produto de uma função trigonométrica inversa a gente resolve pelo método: integração por partes
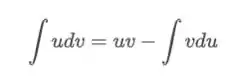
No nosso caso e , assim
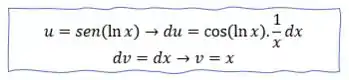
E aplicando por partes na nossa integral temos:
Beleza?
Não era para ficar uma integral mais simples? O que aconteceu no meio??
Sem desespero! Vamos aplicar o método por partes de novo! Isso acontece quando temos funções periódicas! Mas calma, vai dar bom! Confia!
Passo 3
Chegamos a esse resultado aqui
Agora nossa integral recaiu em outra integral! E nela vamos usar por partes! Vamos usar a mesma lógica na escolha de e :
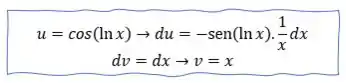
Vamos aplicar a técnica de integração por partes:
Será que fizemos alguma coisa errada? Apareceu de novo aquela integral do seno com logaritmo! Mas calma, vamos arrumar os sinais com cuidado:
Olha só! Temos as duas integrais! isso significa que podemos juntar!
E agora isolar a integral que queremos:
Falta alguma coisa? SIM: somar a constante de integração no final!
Assim temos que:
E é isso! Espero ter ajudado!