UFSC – Cálculo 1 – Lista 4.8 – Questão 1q
Calcule as integrais abaixo.
Passo 1
E aí pessoal, tudo bem?
Essa questão integral complicada, mas vou ajudar você aqui! O problema nos deu essa integral trigonométrica para resolver:
essa é um caso muito especial de integração. No nosso material está em “Métodos de Integração – Parte II: Integrais trigonométricas”, mas especificamente no caso 5:
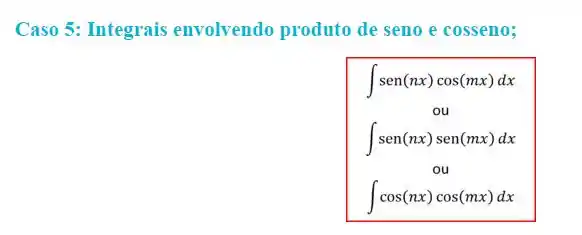
e como resolvemos esses tipos de integrais? Usando as seguintes identidades trigonométricas:
Então a ideia aqui é transformar esse integrando que é um produto de trigonométricas em soma de funções trigonométricas, muito mais simples para integrar!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Precisamos integrar a seguinte coisa:
Então estamos no caso em que temos
Com e . Usando a segunda identidade
E aí nosso integrando fica assim:
Tudo bem até aqui? Nossa missão agora é calcular a integral! Vamos lá?
Passo 3
A integral que temos para resolver é:
Integrando temos:
Acabou por aqui? Não! Precisamos aplicar nos limites de integração, nossa integral aqui é DEFINIDA!
Passo 4
A integral definida que vamos resolver é
E usando o resultado do passo anterior, podemos aplicar os limites de integração:
Aí temos o seguinte:
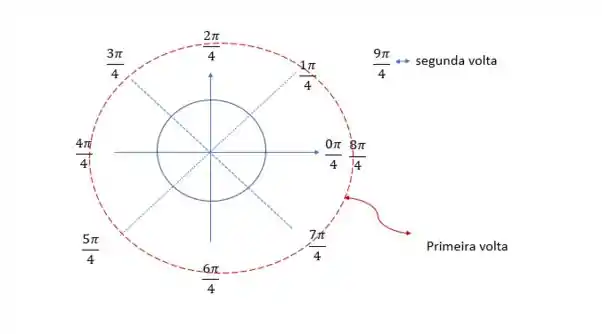
Na primeira volta, partindo do (que é zero) e andando de em , vemos que o ângulo de está no terceiro quadrante, então o seno é negativo e vale .
Continuando nossa volta em torno do ciclo, depois de fechar a primeira volta em , andamos mais chegando em , no primeiro quadrante. Ali o seno é positivo e vale .
Então nosso resultado final fica assim:
E é isso!
Espero ter ajudado! Vamos para a próxima?