Passo 1
(a) O cálculo da carga é uma integral, direta:
E quem é ? Vamos ver:
Substituindo:
Passo 2
(b) Fazendo lei de Gauss nessa região, podemos encontrar o campo elétrico quando :
Passo 3
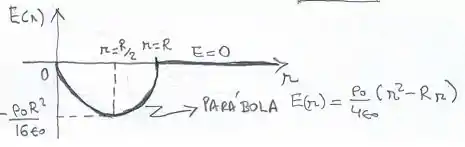
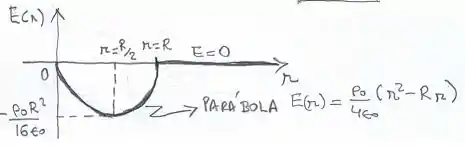
(c) Quando o raio é maior que , temos a carga total dentro da superfície gaussiana. Então, a quação do campo fica bem parecida com aquela equação estudada em cargas puntiformes:
Voltemos à letra (a), passo 1, a carga total é lá obtida quando tomamos :
Então, como não temos cargas dentro da gaussiana, o campo elétrico é, na verdade, nulo.
Passo 4
Resposta
Letra (a)
Letra (b)
Letra (c)
Letra (d)
Exercícios de Livros Relacionados
A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui