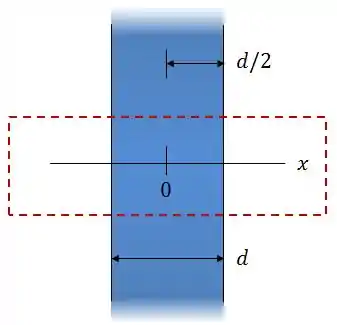
A figura mostra uma seção reta de uma placa não-condutora muito extensa com uma espessura e uma densidade volumétrica de cargas uniforme .
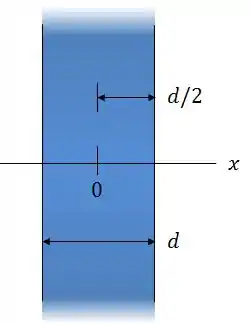
A origem do eixo está no centro da placa.
Determine o módulo do campo elétrico em:
- ;
- ;
- ;
- ;
Passo 1
Beleza! Aqui já está na cara que vamos ter que usar a Lei de Gauss pra facilitar a nossa vida.
Como estamos trabalhando com uma placa, pra facilitar a nossa vida, vamos usar uma simetria planar. Beleza, show! Mas como assim?!
É o seguinte, para esse tipo de simetria (ou toda vez que o problema te falar em placas carregadas, ou chapas), uma boa gaussiana é um cilindro com o eixo perpendicular à chapa.
Eu sei que pode parecer doideira, mas é o melhor caminho pra resolver o problema.
Bom, a gaussiana tem mais ou menos essa cara aqui, quando olhamos de lado:
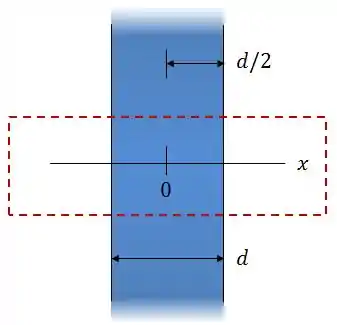
Por causa desse tipo de geometria, o fluxo elétrico através da parede perpendicular à chapa é igual a zero. Assim, só importa para nós o fluxo através das “tampas” do nosso cilindro.
Matematicamente, a Lei de Gauss é a seguinte fórmula:
E como nas tampas da nossa gaussiana, o campo elétrico é constante e perpendicular à superfície (logo, é paralelo a ), podemos reescrever a Lei de Gauss dessa maneira:
Onde a área vai ser sempre a área da tampa do nosso cilindro.
Obs: Ah! Se você estiver se perguntando “Credeuspai! Porque apareceu esse 2 aí na frente?”, lembre-se que o campo elétrico flui através das duas tampas do cilindro, por isso você não pode esquecer de multiplicar por 2, nesse caso!
Organizando essa bagunça, o campo elétrico vai ser dado por:
Agora temos que associar a carga com a nossa gaussiana. Vou fazer isso no próximo passo para fazer um apelo dramático.
Passo 2
Como o problema se trata de uma densidade volumétrica de carga , vamos fazer o seguinte.
Onde corresponde ao “volume de cargas” dentro da nossa gaussiana.
Logo:
Passo 3
- ;
- ;
- ;
- ;
Quando é como se a nossa gaussiana simplesmente não existisse.
Assim, mesmo que não soubéssemos a fórmula, é intuitivo que:
Passo 4
Para esse valor de , a nossa gaussiana está toda no interior da placa.
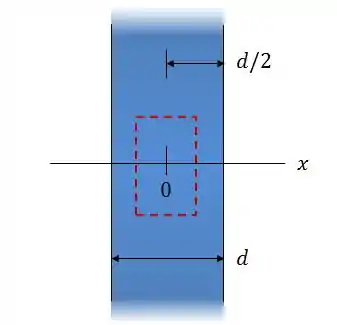
Sabemos que o campo elétrico é dado por:
Nesse caso, é dado por . Onde é a altura do cilindro que escolhemos como gaussiana, que vai depender do que o problema te pedir.
Substituindo de volta na fórmula, vemos que o campo elétrico é dado por:
Agora sim, podemos ser felizes!
;
;
;
Portanto:
Passo 5
Para esse valor de , a nossa gaussiana vai de borda a borda da placa.
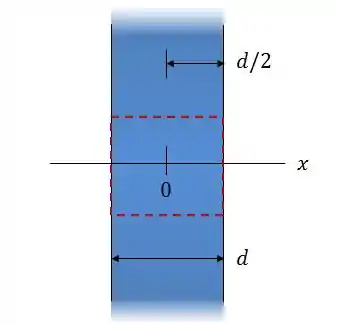
Nesse caso, o raciocínio é o mesmo Passo 4.
Onde
;
;
;
Portanto:
Passo 6
Nesse caso, a gaussiana tem altura maior que a espessura da placa.
Agora, concorda que, a partir do momento que a gaussiana “sai” do interior da placa, a carga interna permanece sempre constante?
Isso significa que o “volume de cargas” no interior da gaussiana permanece constante e igual a . Logo:
Onde:
;
;
;
Portanto:
Isso mostra que, fora da chapa, o campo elétrico permanece constante, independente da distância.
Resposta
- ;
- ;
- ;