PUC-RIO – Física 3 2020.1 – P3– Questão 2
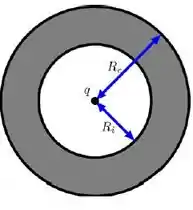
Considere uma carga pontual q posicionada no centro de uma casca esférica isolante de raio interno e raio externo. A casca possui uma carga total distribuída homogeneamente em seu volume.
A Figura serve como guia.
a) Calcule a razão para que o módulo do campo elétrico a uma distância do centro seja nulo (não esqueça o sinal).
Ou seja,
b) Calcule a razão para que o módulo do campo elétrico a uma distância do centro seja nulo (não esqueça o sinal). Ou seja, .
Passo 1
Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?
Letra (a):
Vamos começar imaginando uma superfície de Gauss esférica de raio e concêntrica a esfera do problema. Usando a lei de Gauss temos:
E é a carga interna a essa superfície. Podemos escrever essa carga como a soma da carga mais uma porção que está compreendida por essa superfície:
Estamos interessados em e devemos considerar o que implica em .
Agora vamos calcular :
E agora voltando ao :
Passo 2
Letra (b):
Usando a lei de Gauss temos:
Mas agora o raio da superfície gaussiana é . Vamos determinar :
Beleza?
Pronto pra próxima questão? =)