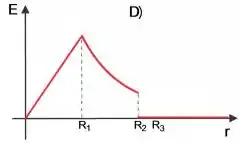
Uma esfera isolante de raio possui uma carga uniformemente distribuída em todo o seu volume. Esta esfera é concêntrica a uma casca esférica condutora de raio interno e raio externo que é carregada com uma carga tal como indicado na figura.
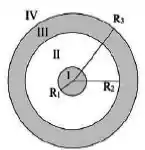
O gráfico que melhor descreve o campo elétrico nas regiões I a IV é:
Passo 1
Beleza, esse é um problema clássico de Lei de Gauss, que é dada por:
A ideia aqui é a seguinte, vamos aproveitar a simetria esférica do problema e escolher uma gaussiana também esférica.
Fazendo isso, garantimos, em todos os pontos da gaussiana, que o módulo do campo elétrico é constante, e que os vetores e são paralelos. Como resultado, podemos escrever a Lei de Gauss da seguinte forma:
Onde corresponde à área da superfície gaussiana.
Assim, o nosso trabalho aqui é, para cada região, determinar a carga interna .
Passo 2
- Região :
- Região :
Essa região corresponde ao interior da esfera carregada com carga uniformemente em todo o seu volume. Dessa forma, podemos usar a definição de densidade volumétrica de carga uniforme:
Substituindo na expressão do campo elétrico, teremos:
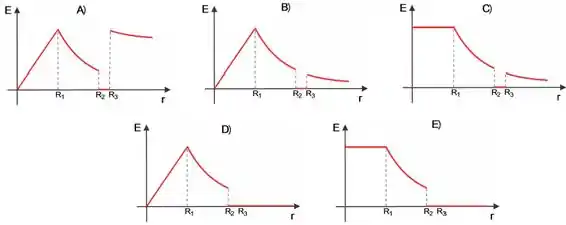
Nessa região, o campo cresce linearmente de acordo com a variável . Com isso, já podemos eliminar as alternativa e .
Passo 2
Podemos repetir o cálculo para todas as outras regiões, mas vamos dar uma olhada nas opções que nos sobraram:
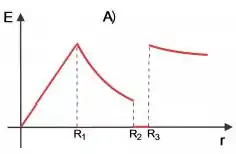
Em todas as opções, o campo nas regiões e são extamente iguais. Dessa forma, podemos ser malandos e partir direto pra região .
Nessa região, a gaussiana engloba todo o sistema, então a carga será a soma das cargas na esfera (de raio ) e na casca esférica (de raios e ). Logo:
Finalmente:
A resposta certa é a letra .
Passo 3
Caso quiséssemos calcular os campos para as regiões e , a ideia seria a seguinte: para a região , (que corresponde à carga de toda a esfera de raio ), e para a região , basta lembrar que o campo elétrico no interior de um condutor é sempre nulo.
Logo:
Resposta