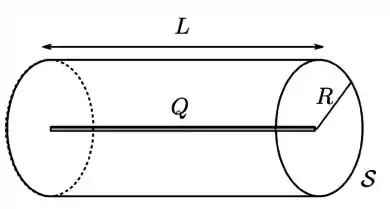
Um fio fino, retilíneo e finito de comprimento está uniformemente carregado com uma carga total . Desenha-se então uma superfície fechada na forma de um cilindro reto de raio e comprimento , como mostrado na figura abaixo. O cilindro é posicionado de forma que seu eixo coincida com o eixo do fio e os centros de suas tampas toquem as extremidades do fio.
- O campo eletrostático produzido pelo fio é perpendicular a todos os pontos da superfície lateral do cilindro? Justifique.
- O campo eletrostático produzido pelo fio tem a mesma intensidade sobre todos os pontos da superfície lateral do cilindro? Justifique.
- É possível utilizar a lei de Gauss em conjunto com a superfície para se obter uma expressão para o campo eletrostático produzido pelo fio em todo o espaço? Justifique.
Passo 1
Na Figura abaixo, consideramos apenas o fio finito para analisarmos e relembrarmos de algumas características. O eixo passa pelo meio do fio e é perpendicular a ele e o ponto está sobre esse eixo de simetria a uma distância do centro do fio.
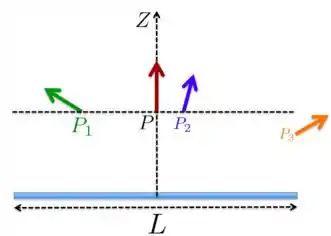
A gente viu que esse campo elétrico produzido por um fio uniformemente carregado finito sobre o é
Ou seja, nesse ponto , que está no eixo de simetria do fio, o campo elétrico tem componente apenas na direção de .
Se tomamos outros pontos, como aqueles e da Figura acima, teremos um campo elétrico apontando numa direção arbitrária. Nesse caso, como você pode ver na Figura, os campos terão componentes nas duas direções e (paralela) e também terão intensidades diferentes em pontos diferentes.
Então, vamos resumir essas características:
- O campo elétrico sobre o eixo de simetria do fio FINITO aponta apenas na direção e a sua intensidade muda com a distância ;
- Em outros pontos, como e , os campos têm direções arbitrárias com componentes em ambas direções e ;
- O módulo desses campo, ou seja, a intensidade deles, têm valores diferentes sobre diferentes pontos fora do eixo de simetria acima e abaixo do fio FINITO;
Beleza até aqui?
Passo 2
a) Agora, vamos “vestir” esse fio FINITO com o cilindro da Figura do enunciado.
A gente acabou de discutir e ver que o campo não é perpendicular a todos os pontos do espaço, pois esse campo pode ter componentes tanto na direção quanto na direção . A componente desse campo que está na direção de não contribui para o fluxo elétrico, pois forma um ângulo de com o vetor normal à superfície.
Portanto, o campo elétrico produzido pelas cargas do fio FINITO não será sempre perpendicular à superfície do cilindro.
Passo 3
b) Do que a gente discutiu, vimos também que o campo elétrico não terá os mesmos valores em todos o pontos sobre a superfície desse cilindro. Além disso, o campo elétrico nas tampas desse cilindro também não será tangente às respectivas áreas. Ou seja, nas tampas do cilindro, teremos também campo elétrico perpendicular às áreas.
Passo 4
c) Agora a gente mata tudo de vez!! ;-)
Como o campo elétrico tem componentes em ambas as direções e , não tem o mesmo valor sobre a superfície lateral do cilindro e, além disso, tem também componentes perpendiculares às tampas, não conseguimos tirar o campo elétrico da integral na lei de Gauss para obter o valor do campo.
Por isso, não é possível utilizar a lei de Gauss para obter o valor do campo elétrico produzido por esse fio FINITO.
Resposta
- Não, pois o campo também tem componentes paralelas ao eixo do cilindro em outros pontos fora do eixo de simetria.
- Não, pois pontos fora do eixo de simetria têm intensidades do campo diferentes.
- Não, pois os valores do campo mudam em pontos diferentes da superfície e também tem componentes perpendiculares às tampas do cilindro.