Lei de Gauss
Próximo a um plano (infinito) , com densidade superficial de carga , temos três sistemas, todos com a mesma carga elétrica (não nula):
uma partícula (pontual);
um sólido uniformemente carregado;
uma chapa bidimensional, também uniformemente carregada;
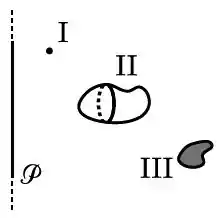
Assinale a opção que melhor indica a relação entre os módulos das forças elétricas devidas ao plano sobre cada um dos sistemas.
.
.
.
.
.
Passo 1
O campo elétrico gerado por um plano infinito é dado por:
Assim, chamando de a carga dos três sistemas, as forças elétricas serão dadas por:
Ou seja, como o plano é infinito, o campo elétrico não depende da distância do sistema e a força elétrica vai depender somente da carga e não da geometria dos mesmos.
Portanto:
A resposta certa é a letra .
Resposta
.
Exercícios de Livros Relacionados
A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui