Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Gauss – Simetrias

Ver Teoria
Exercício 201234567891011121314151617181921222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Lei de Gauss

Considere duas placas finas, planas, infinitas, situadas nos planos cartesianos z = 0 e z = L > 0 , com densidades superficiais de carga iguais a – σ e 2 σ , respectivamente, onde σ = c o n s t . Assinale a opção que indica as expressões corretas para o vetor campo elétrico nas regiões

  1. z < 0
  2. 0 < z < L
  3. z > L
  1. 0 , σ / ϵ 0 z ^ , 0
  2. 0 , - ( σ / ϵ 0 ) z ^ , 0
  3. [ σ / ( 2 ϵ 0 ) ] z ^ , [ 3 σ / ( 2 ϵ 0 ) ] z ^ , - [ σ / ( 2 ϵ 0 ) ] z ^
  4. - ( σ / ϵ 0 ) z ^ , - ( 3 σ / ϵ 0 ) z ^ , ( σ / ϵ 0 ) z ^
  5. - [ σ / ( 2 ϵ 0 ) ] z ^ , [ - 3 σ / ( 2 ϵ 0 ) ] z ^ , [ σ / ( 2 ϵ 0 ) ] z ^

Passo 1

Vamos calcular rapidamente o campo feito por um plano infinito utilizando a Lei de Gauss:

∯ G E → ∙ d A → = Q i n t ϵ 0

Como se trata de uma múltipla escolha, não precisamos justificar nada, mas vamos fazer direitinho para não nos confundirmos. Escolhendo uma Gaussiana cilíndrica, temos que o fluxo elétrico se dá tanto pela “tampa” do cilindro quanto pela “base”, portanto a área é 2 A :

E ( 2 A ) = Q i n t ϵ 0

A carga interna está relacionada com a densidade pela fórmula:

σ = Q i n t A → Q i n t = A σ

E ( 2 A ) = A σ ϵ 0

E = σ 2 ϵ 0

Passo 2

Agora é só desenhar os campos de cada plano e somar:

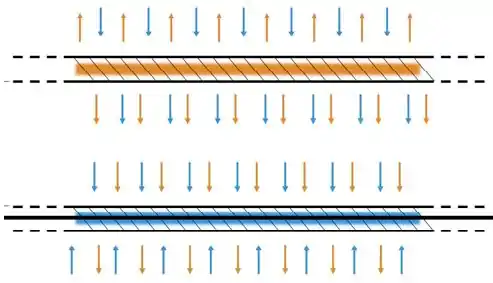
  1. Para z < 0 :

    2. E → = σ 2 ϵ 0 z ^ - σ ϵ 0 z ^

    E → = - σ 2 ϵ 0 z ^

  2. Para z ∈ [ 0 , L ] :

    3. E → = - σ 2 ϵ 0 z ^ - σ ϵ 0 z ^

    E → = - 3 σ 2 ϵ 0 z ^

  3. E finalmente, para z > L :

E → = σ ϵ 0 z ^ - σ 2 ϵ 0 z ^

E → = σ 2 ϵ 0 z ^

Resposta

Letra e.

Exercícios de Livros Relacionados

A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui