Uma esfera isolante de raio possui densidade volumétrica de carga não uniforme dada pela função , onde a constante vale . O sistema de coordenadas está indicado na figura (o eixo sai do plano da figura). Use .
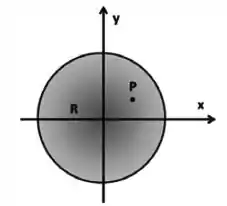
Adote uma superfície gaussiana esférica centrada na origem e de raio . Use-a para calcular o módulo do campo elétrico produzido em todos os pontos a da origem.
Calcule, utilizando o resultado do item anterior, o vetor campo elétrico no ponto de coordenadas ().
Suponha agora que uma caixa cúbica condutora de paredes espessas, carregada com carga líquida , seja colocada de forma a envolver totalmente nossa esfera isolante e eventualmente outras cargas. Suponha que a carga total da esfera isolante seja . Medindo-se toda a quantidade de carga presente na superfície externa da caixa metálica encontrou-se .
Existem outras cargas, além da esfera isolante, na caixa metálica? Justifique sua afirmação e, em caso de resposta afirmativa, calcule o valor total destas outras cargas.
Passo 1
Pela Lei de Gauss, temos:
Como o corpo em questão é esférico e nossa gaussiana também, o campo será sempre paralelo à superfície, e também será constante, logo:
Agora, falta só definir a nossa carga interna!
Agora é só substituir na equação do campo!
Passo 2
Para determinar o campo no ponto , precisamos determinar a que distancia ele está da origem! Podemos ver que se trata de um triangulo , mas se você não viu isso....tranquilo, é só fazer um Pitágoras que sai!
Show! Essa é a distância que calculamos no item ! Agora é só determinar as componentes!
Onde é o ângulo do triângulo e é o campo calculado no item :
Portanto, o campo em é:
Passo 3
Para determinar se existem outras cargas dentro da caixa metálica, podemos usar o fato de que o campo no interior de um condutor é nulo. Ou seja, se traçarmos uma gaussiana que envolva apenas a parte interna da caixa, a soma de cargas deve ser nula, pois o campo é necessariamente nulo!
Vamos começar determinando a carga na parte interior da caixa. Como temos que a caixa está carregada com carga e superfície externa apresenta , temos:
Agora é só substituir para determinar :
Resposta