A figura a seguir é uma seção de uma barra condutora de raio e comprimento no interior de uma casca coaxial, de paredes finas, de raio e mesmo comprimento .
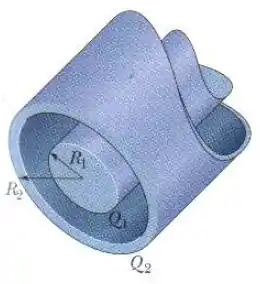
A carga da barra é ; a carga da casca é . Determine:
- O módulo do campo elétrico a uma distância radial ;
- A direção (para dentro ou para fora) do campo elétrico a uma distância radial ;
- O módulo do campo elétrico a uma distância radial
- A direção (para dentro ou para fora) do campo elétrico a uma distância radial ;
- A carga na superfície interna da casca;
- A carga na superfície externa da casca;
Passo 1
- O módulo do campo elétrico a uma distância radial ;
- A direção (para dentro ou para fora) do campo elétrico a uma distância radial ;
- O módulo do campo elétrico a uma distância radial ;
- A direção (para dentro ou para fora) do campo elétrico a uma distância radial ;
- A carga na superfície interna da casca;
- A carga na superfície externa da casca;
Show de bola! Se , significa que estamos querendo calcular o campo elétrico fora do meu sólido.
Como se trata de um cilindro, podemos escolher como a nossa gaussiana um cilindro de raio e comprimento , assim a gente resolve a nossa vida.
Matematicamente, a Lei de Gauss é a seguinte fórmula:
E como no cilindro que nós escolhemos como gaussiana, o campo elétrico é constante e perpendicular à superfície, podemos reescrever a Lei de Gauss dessa maneira:
Foi tranquilo até aqui?
Passo 2
Bom, agora vamos ver o que falta pra encontrarmos o valor do campo elétrico.
Lembrando que a nossa gaussiana se trata de um cilindro de raio e de comprimento , a área superficial é dada por
Onde:
;
;
Como a nossa gaussiana engloba todo o fio condutor, a carga interna total vai ser igual à soma das cargas da barra com a casca. Sendo assim:
Onde:
;
;
Agora é só jogar na fórmula que encontramos:
Lembrando que .
Como estamos interessados no módulo do campo elétrico:
Passo 3
Lembra que no item anterior, quando calculamos o campo elétrico nós encontramos um valor negativo?
Isso aconteceu porque a carga interna total da nossa gaussiana é negativa.
Portanto, o campo elétrico vai estar na direção radial, apontando para dentro da gaussiana.
Passo 4
O raciocínio é o mesmo que usamos anteriormente. Então, a nossa gaussiana vai ser um cilindro de raio e de comprimento .
Assim, a área lateral vai ser dada por:
Onde:
;
;
A diferença agora é que, analisando os dados do problema, agora a nossa gaussiana vai ser um cilindro que vai estar entre a barra e a casca.
Entretanto, como a única carga que nos interessa, de acordo com a Lei de Gauss, é a carga no interior da gaussiana, a carga interna total agora vai ser
Agora, novamente, é só jogar na fórmula:
Passo 5
Lembra que no item anterior, quando calculamos o campo elétrico nós encontramos um valor positivo?
Isso aconteceu porque a carga interna total da nossa gaussiana é positiva.
Portanto, o campo elétrico vai estar na direção radial, apontando para fora da gaussiana.
Passo 6
O que acontece é o seguinte... se não tivesse nenhuma carga no interior da casca, quando olhássemos de frente, as cargas na casca carregada teriam essa distribuição:
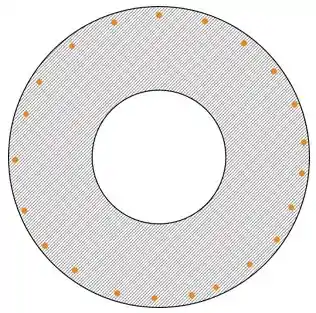
Mas como existe carga no interior da casca carregada, haverá uma distribuição parecida com esta:
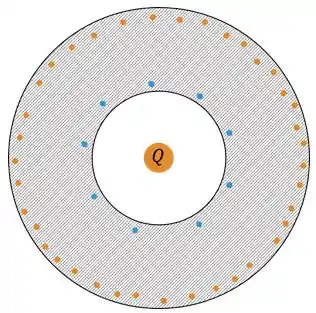
Isso acontece porque a carga no interior atrai o mesmo número de cargas que correspondente ao seu valor, mas de sinais opostos.
Assim, se no interior da casca existe a barra de carga , na superfície interna da casca, haverá uma carga de
Passo 7
Vamos continuar o raciocínio do item anterior, ok?
Já sabemos que a casca possui uma carga de , certo? (tá no enunciado)
Então não importa como as cargas estejam distribuídas na casca cilíndrica, a carga total deve ser sempre a mesma .
Isso significa que:
Resposta
- ;
- Direção radial, para dentro da gaussiana;
- ;
- Direção radial, para fora da gaussiana;