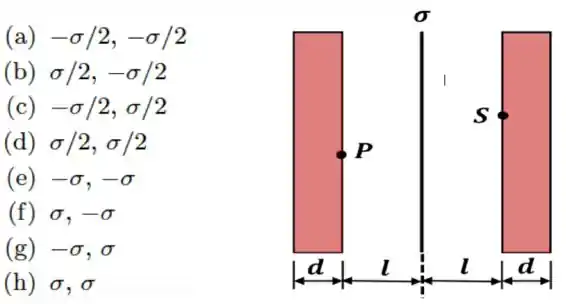
Duas placas condutoras infinitas, neutras, possuem espessura e encontram-se a uma mesma distância de um plano infinito, de espessura desprezível, carregado com uma densidade superficial de carga , como mostrado na figura abaixo. As três placas encontram-se em equilíbrio eletrostático. Nessa situação, as densidades superficiais de cargas nos pontos e indicados na figura, localizados sobre as superfícies das placas mais próximas do plano, valem, respectivamente:

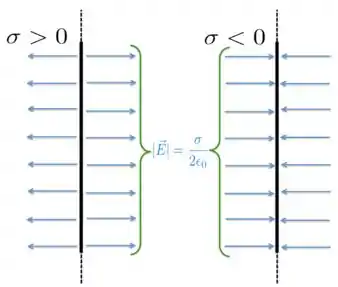
Para uma placa infinita com densidade de carga , o campo elétrico que ela produz é perpendicular à placa e tem o mesmo módulo em toda a região, tanto à direita da placa, quanto à sua esquerda. Se a carga é positiva, as linhas de campo se afastam da placa, e se são negativas, sem aproximam dela, como mostra a figura abaixo.

Vamos analisar o caso em que a distribuição superficial de carga é positiva, ou seja, , como mostra a figura abaixo (a análise para o caso para é idêntica e a resposta não depende do sinal da carga !).

Nesse caso, a gente sabe que as linhas de campo se afastam da placa e que saem da carga positiva () e chegam em uma carga negativa (cujo valor ainda não sabemos qual é!), correto?

Beleza!! Então esse campo elétrico produzido por induz, nas placas condutoras em vermelho, cargas negativas que ficarão localizadas em suas superfícies. Até aqui, tá tudo OK? Agora qual o valor dessas cargas na superfície?

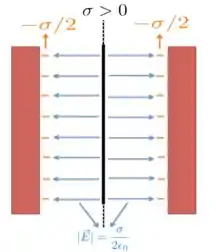
Como a gente viu, o campo elétrico, tanto à direita de , quanto à sua esquerda, tem módulo igual à , como colocamos na figura acima. Ou seja, em toda a região esse entre as placas em vermelho, esse é o valor do módulo campo elétrico, INCLUSIVE EXATAMENTE SOBRE A SUPERFÍCIE DOS CONDUTORES EM VERMELHO!

Portanto, já temos duas informações importantes:

1. A CARGA SOBRE A SUPERFÍCIE DOS CONDUTORES EM VERMELHO É NEGATIVA;
2. O MÓDULO CAMPO ELÉTRICO SOBRE TODOS OS PONTOS DA SUPERFÍCIE DOS CONDUTORES EM VERMELHO É IGUAL A:

Agora, qual o valor dessas cargas na superfície? Segue o raciocínio...chegaremos lá.

Agora, para fechar com chave de ouro, precisamos de mais uma informação sobre campos elétricos em condutores.

Sabemos que o campo elétrico no interior de um condutor em equilíbrio eletrostático é zero e que qualquer carga em excesso que ele tenha vai se localizar sobre sua superfície.

Particularmente, o campo elétrico produzido pela carga que fica na superfície do condutor tem da seguinte forma geral:

Mas a gente já viu que, no caso do problema que estamos resolvendo aqui, esse campo elétrico sobre a superfície dos condutores em vermelho deve ser tal que temos a seguinte igualdade

Pronto!! Fechou agora? Dessa igualdade a gente descobre o quê?

A DENSIDADE DE CARGA SOBRE O CONDUTOR EM VERMELHO É !

Então, a gente sabe o seguinte: a carga induzida sobre todos os pontos da superfície dos condutores, inclusive nos pontos e , são negativas e tem densidade superficial dada por !!!

Se você repetir a mesma análise acima para o caso em que , você vai chegar à seguinte conclusão: a densidade superficial de carga induzida sobre os condutores é . Ou seja, independente do sinal da densidade de carga , a carga induzida sobre os condutores será dada !!!

Este problema é interessante porque discute propriedades importantes de condutores e te ajuda revisar como é o campo elétrico produzido por uma placa infinita com densidade superficial . Entendendo bem essa solução que discuti com você agora, você mata uma série de outros problema similares... ;-)