A figura abaixo ilustra uma esfera maciça e não-condutora, de raio e densidade volumétrica de carga constante e positiva . Na figura, denota uma distância radial arbitrária ao centro da esfera. Tal esfera está localizada no vácuo, cuja constante de permissividade elétrica é dada por .
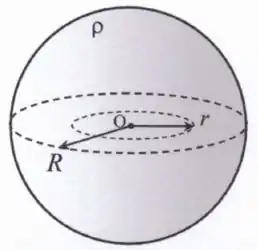
- Calcule o módulo do campo elétrico na região .
- Calcule o módulo do campo elétrico na região .
- Esboce um gráfico qualitativo descrevendo como os módulos dos campos elétricos calculados nos itens (a) e (b) acima variam com a distância , onde .
Passo 1
a) Uma coisa importante aqui é notar que a esfera é feita de material não-condutor. A gente sabe que quando o material é condutor e está carregado, ou seja, possui cargas em excesso, essas cargas ficam distribuídas sobre a superfície do material, mesmo que o objeto seja maciço, e o campo elétrico em é nulo em todos os pontos da esfera.
Esse não é o caso deste problema, já que a carga que a esfera maciça possui fica distribuída uniformemente ao longo de todo o seu volume.
Vamos ver cada caso um dos casos: e .
Para calcular cada um dos campos, vamos utilizar a lei de Gauss, que afirma o seguinte:
ou seja, o fluxo do campo elétrico através da superfície fechada é diretamente proporcional à carga líquida que está no interior de .
Passo 2
a) Para
Vamos começar imaginando uma superfície gaussiana esférica de raio inscrita no volume da esfera. Como , então a carga que está na região produz um campo elétrico que se afasta do centro da esfera.
Além disso, pela simetria do problema, o campo elétrico tem componente apenas na direção radial e tem o mesmo valor em todos os pontos da superfície gaussiana fechada . Então, o campo elétrico é:
mostrando que o campo elétrico é radial.
A área deve ser tomada sempre apontando para fora da superfície gaussiana fechada. Por isso,
ou seja, é um vetor paralelo ao vetor campo elétrico em todos os pontos da superfície gaussiana. Colocando isso no lado esquerdo da lei de Gauss, teremos:
Bom, agora precisamos ver como é o lado direito da lei de Gauss. Como o problema diz que a distribuição de cargas é uniforme e é , isso significa que:
sendo que é a carga total que está no volume .
Uma vez que temos a carga no interior da superfície gaussiana fechada , podemos escrever a lei de Gauss como
o que dá um campo elétrico cujo módulo é
Essa equação mostra que o campo elétrico cresce linearmente com a distância a partir do centro.
Para finalizar, o vetor campo elétrico na região é
Passo 3
b) Para
Para essa região valem os mesmos argumentos de simetria que fizemos para o campo elétrico no caso de , ou seja, é radial e depende apenas da distância a partir do centro da esfera. Por isso, o campo elétrico tem o mesmo módulo em todos os pontos da gaussiana esférica e aponta na direção radial para fora da superfície, já que .
Com isso, o lado esquerdo lei de Gauss será também
Nesse caso, como a nossa gaussiana engloba toda a carga da esfera não-condutora, a carga total dentro da superfície gaussiana esférica será
Juntando as duas últimas expressões, teremos um vetor campo elétrico
Aqui é importante notar o seguinte: essa última expressão mostra que, para , temos um campo elétrico que varia com , que tem o mesmo comportamento do campo gerado por uma carga puntiforme igual a carga total da esfera que estivesse colocada no centro da esfera. Por isso, nesse caso, por causa simetria, é como se a carga total da esfera maciça não condutora estivesse toda localizada em um único ponto, o centro da esfera. Mas fica ligado, isso é para e por causa da simetria esférica do problema!!!
Passo 4
c) Como vimos, para , o campo elétrico comporta-se linearmente com a distância do centro da esfera. Para , o campo elétrico decresce com o aumento de e é proporcional a . Exatamente na superfície, ou seja, onde , os dois campos elétricos têm o mesmo valor e a intensidade correspondente é:
Juntando esses comportamentos em um gráfico, temos o seguinte:
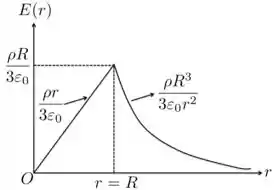
Resposta
- Ver Passo 4.