Uma esfera sólida isolante de raio possui uma densidade de carga uniforme em todo seu volume.
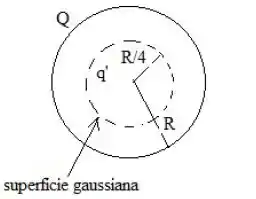
O módulo do campo elétrico a uma distância do centro desta esfera vale:
Passo 1
Para esse tipo de problemas, partimos logo para a Lei de Gauss, dada por:
Ao escolhermos uma superfície gaussiana esférica com raio , garantimos que, em todos os pontos da gaussiana, o módulo do campo elétrico é constante e que os vetores e são paralelos.
Dessa forma, podemos escrever a Lei de Gauss da seguinte forma:
O nosso próximo trabalho é calcular a carga .
Passo 2
Como a carga está uniformemente distribuída no volume, podemos usar o conceito de densidade volumétrica de carga , dada por:
Onde corresponde ao volume da superfície gaussiana, dessa forma:
Substituindo na expressão do campo elétrico, teremos:
Organizando essa bagaça, encontramos o seguinte:
Onde , logo:
Resposta