Um disco circular, fino e isolante de raio possui uma densidade superficial de carga constante, como mostra a figura abaixo.
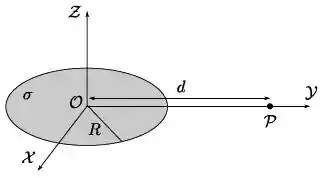
Considere um ponto sobre o eixo , a uma distância do centro do disco. A intensidade do campo elétrico nesse ponto no limite assintótico em que ele está muito afastado do disco, ou seja, quando , é dada por:
Passo 1
Pra resolver essa questão, vamos aplicar a Lei de Gauss, dada por:
Como , podemos tratar o disco carregado como uma carga pontual, sendo assim, vamos escolher uma gaussiana esférica de raio . Dessa forma:
Passo 2
Para determinar a carga do disco, vamos utilizar a densidade superficial de cargas, dada por:
Onde corresponde à área do disco, logo:
Substituindo na expressão do campo elétrico, teremos:
Resposta
Exercícios de Livros Relacionados
A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui