Um cubo isolante de aresta encontra-se uniformemente carregado em todo o seu volume e possui uma carga total . Desenha-se, então, uma superfície fechada , também cúbica e de aresta (), concêntrica ao cubo original e com faces paralelas ao mesmo, como mostra a figura abaixo.
- O campo elétrico produzido pelo cubo tem a mesma intensidade em todos os pontos da superfície ? Justifique.
- O campo elétrico produzido pelo cubo é perpendicular à superfície em todos os seus pontos?
- Podemos usar a lei de Gauss em conjunto com a superfície para obter explicitamente uma expressão para o campo elétrico produzido pelo cubo na região fora dele? Justifique.
Passo 1
a) Olhando para a figura, vemos que existem pontos da superfície fechada que estão a distâncias diferentes da carga . Por exemplo, olhando para a figura abaixo, as retas em azul, que representam os vetores campos elétricos, são perpendiculares às arestas do cubo de carga e estão à mesma distância de .
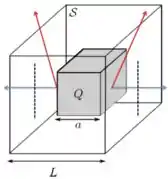
Por outro lado, os vetores em vermelho, que estão no mesmo plano das azuis, mas inclinadas em relação a estas, atravessam os pontos das “quinas” do cubo e por isso estão a uma distância maior do cubo . Disso, concluímos que o módulo campo elétrico nesses pontos é menor do que aquele que a carga produz nas posições onde as retas azuis tocam as faces de .
Por isso, a resposta deste item é NÃO.
Passo 2
b) A gente pode olhar para as mesmas retas que desenhamos no caso do item a) para ver que a resposta para esse caso também é NÃO.
Para as retas azuis, os respectivos campos elétricos apontam numa direção perpendicular a cada uma das faces. Já para retas em vermelho, os campos, além de terem módulos diferentes, também estão em uma direção inclinada com relação às azuis e, portanto, não são perpendiculares às superfícies.
Passo 3
c) Se juntamos as duas conclusões que tiramos nos itens a) e b) acima, vemos que NÃO é possível utilizar a lei de Gauss para obter uma expressão para o módulo do campo elétrico neste caso, pois seu módulo não é o mesmo em todos os pontos da gaussiana cúbica e seu ângulo com relação à superfície muda para os diferentes pontos de cada face do cubo.
Resposta
- Não, pois os pontos da gaussiana estão a distâncias diferentes da carga ;
- Não, o vetor campo elétrico tem direções diferentes ao longo das faces da gaussiana cúbica ;
- Não, pois o módulo do campo elétrico não é o mesmo sobre a gaussiana e a direção e sentido dele mudam ao longo de cada face da superfície fechada.